Le trait caractéristique de la machine à combustion est la relation fonctionnelle existant entre l’accroissement de puissance fournie à de telles machines et l’accroissement du pouvoir des ouvriers à accomplir un travail. A partir de l’examen de cette relation fonctionnelle, Gottfried Leibniz (1646-1716) a défini les notions de puissance, de travail et de technologie au sein même de la Science Physique.
L’étude de cette relation fonctionnelle, étendue à partir du cas spécifique de la machine à combustion à tous les autres aspects du processus de production, constitue le sujet de l’économie physique. L’économie physique est une partie intégrante de la Science Physique prise dans son ensemble ; l’étude de l’économie politique, constamment gouvernée par les principes de l’Economie Physique, est la science économique.
Le contexte pratique du développement par Leibniz de la science économique était son intention de révolutionner l’exploitation minière, les manufactures et le transport fluvial par l’emploi généralisé de machines à vapeur au charbon.
Le collaborateur de Leibniz, Denis Papin (1647-1714), a été le premier à développer une machine à vapeur efficace, qui a propulsé efficacement un bateau sur une rivière [1]. Leibniz expliquait que le développement de la production industrielle par des machines à vapeur alimentées au charbon exigeait une amélioration qualitative dans l’exploitation des mines de charbon et de fer. Cette amélioration impliquait l’application de la machine à vapeur à des exploitations minières, telles le pompage de l’eau, comme condition préalable à l’application des potentialités du charbon à la production industrielle.
Cela a été le cœur du programme économique que Leibniz a fourni à la Russie de Pierre 1er ; c’est pourquoi la Russie a progressé au point que son rythme de développement minier et manufacturier au cours du XVIIIe siècle a surpassé celui de la Grande-Bretagne.
La révolution dans l’exploitation minière inspirée par l’influence de Leibniz s’est étendue depuis les centres caméralistes de l’Allemagne jusqu’en Amérique du Nord et du Sud et même jusqu’au Japon [2].
Bien que le premier écrit de Leibniz au sujet de l’économie politique Société et Economie date de 1671, ses travaux sur les machines à vapeur ont véritablement commencé à Paris au cours de la période 1672-1676, pendant laquelle il se trouvait auprès de l’Académie des Sciences, institution fondée par Jean-Baptiste Colbert (1619-1683), l’associé et le successeur de Mazarin.
Parmi les collaborateurs de Leibniz les plus remarquables au cours de cette période, on trouve un autre protégé de Colbert, Christiaan Huyghens (1629-1695), dont la conception des machines à combustion est à l’origine des principes des moteurs à explosion à essence et à diesel.
Le développement des machines à vapeur modernes date des travaux de Léonard de Vinci (1452-1519) à la fin du XVe siècle. L’effort pour développer le charbon comme combustible industriel fut entamé à la fin du XVIe siècle par les cercles anglais associés au grand scientifique William Gilbert (1544-1603) [3].
Plus fondamentalement encore, au regard du développement par Leibniz de la science économique, Léonard a aussi élaboré les principes de la conception de machines, jetant la base des travaux de Huyghens, de Leibniz et, plus tard, de l’Ecole Polytechnique de Lazare Carnot (1753-1823) et de Gaspard Monge (1746-1818).
Le principe de moindre action de Leibniz, qui se trouve au centre de sa définition du concept de « technologie » (ou de « polytechnique », selon l’expression française d’alors), est dérivé des principes géométriques de la conception de machines employés par Léonard.
Le principe de moindre action est si central à la science économique qu’il faut ajouter ici quelques mots sur le développement de ces principes géométriques.
Relativement à toute période connue de l’Histoire, la rapidité du développement de la science physique en Europe, du XVe au milieu du XIXe siècle, est supérieure de plusieurs ordres de grandeur à celle de toute autre période ou de toute autre branche de la culture humaine.
Dans la mesure où ce développement puisse être porté au crédit des contributions d’un seul savant, l’on peut dire qu’aucune des découvertes de la physique mathématique moderne, en particulier, n’aurait pu être possible sans l’œuvre du Cardinal Nicolas de Cues (1401-1463) que ses écrits comme De la docte ignorance, firent connaître dans toute l’Europe et au-delà. Le Cusain émit une hypothèse héliocentrique qui, dans une version modifiée, a été employée et prouvée par Johannes Kepler (1571-1630), le fondateur de la physique mathématique moderne [4].
Plus directement encore aux origines du principe de moindre action de Leibniz, Nicolas de Cues opéra une révolution dans la géométrie, en reconsidérant dans son intégralité le problème de la quadrature du cercle posé par Archimède (environ 287-212 av. J-C). Il annonça qu’il avait découvert une méthode supérieure à celle d’Archimède, découverte connue aujourd’hui sous l’appellation de théorème isopérimétrique en topologie, appelé par le Cusain le principe du minimum-maximum [ Appendice 1 ].
Cette découverte est à la base du principe de moindre action de Leibniz, la clé pour la mesure de toute technologie (polytechnique).
La même découverte, sous sa forme plus avancée employée par Karl Gauss (1777-1855), Lejeune-Dirichlet (1805-1859) et Bernhard Riemann (1826-1866), est à la base de la méthode LaRouche-Riemann d’analyse économique, le sujet de ce livre.
Avant la production en Egypte de ce que l’on connaît aujourd’hui sous le nom des treize livres d’Euclide, Les éléments, la géométrie grecque classique était, suivant notre terminologie contemporaine, une géométrie synthétique. Il s’agit d’une forme de géométrie qui exclut tous les axiomes, les postulats et les méthodes déductives formelles d’obtention des preuves associés aux théorèmes d’Euclide.
La seule forme d’existence auto-évidente [self-evident], en géométrie synthétique, est l’action circulaire ; les définitions de la ligne droite et du point sont dérivées du pliage d’un cercle sur lui-même. En géométrie, toute figure doit être construite en n’utilisant rien d’autre que la seule action circulaire, plus la droite et le point ainsi définis.
La redécouverte par Nicolas de Cues que l’action circulaire est une forme d’existence soi-évidente dans l’espace visible, la preuve isopérimétrique, a révolutionné la géométrie européenne parmi les successeurs du Cusain tels Luca Pacioli (1450-1520) et le collaborateur de Pacioli, Léonard de Vinci.
Les travaux du Cusain, de Pacioli, de Léonard et des successeurs de Léonard, tels Albrecht Dürer (1471-1528) et l’Ecole de Raphaël (Raffaelo Sanzio, 1483-1520), ont constitué la base des travaux de Kepler, de Gérard Desargues (1591-1661), de Pierre Fermat (1601-1665) et de Blaise Pascal (1623-1662), tous contributeurs à l’œuvre de Leibniz, directs ou indirects mais essentiels.
Les travaux de Gauss, Dirichlet et Riemann sont basés sur cette même méthode géométrique [5].
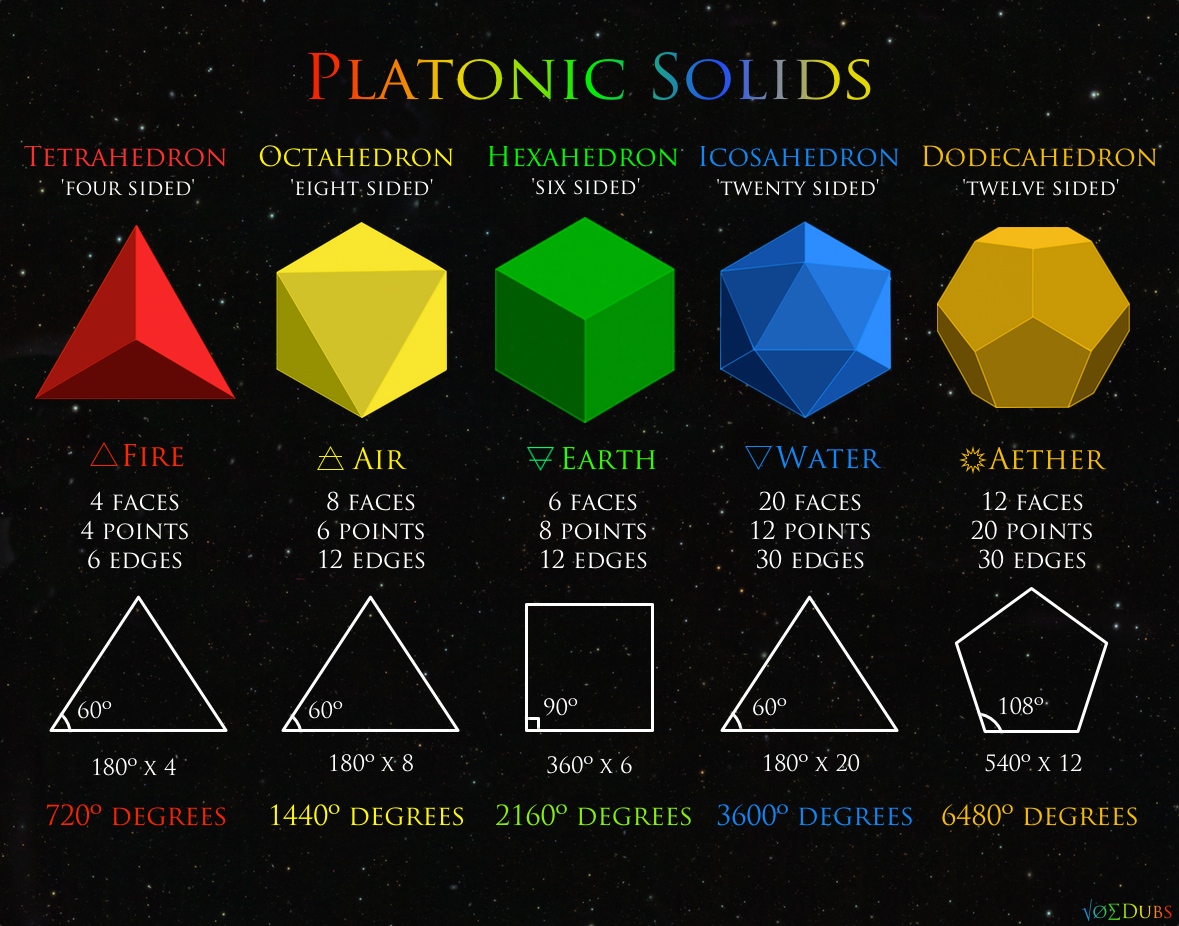
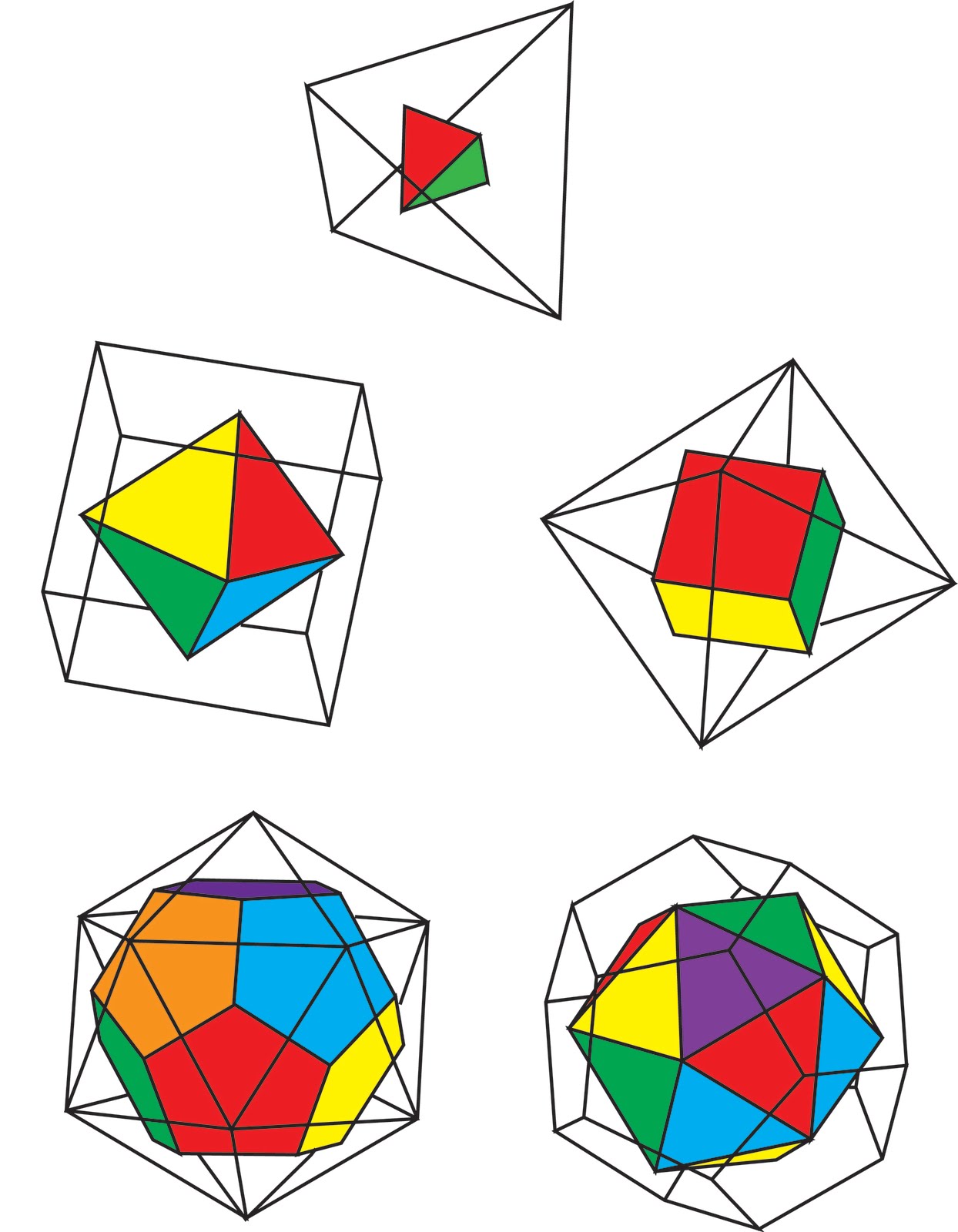
Le sujet principal des travaux sur la géométrie de Pacioli et de Léonard, a porté sur la maîtrise du principe des cinq solides platoniciens extrait du Timée [6] de Platon (environ 427-347 av. J-C). C’est la preuve que dans l’espace visible (« Euclidien »), seules cinq espèces de polyèdres réguliers peuvent être construites par les méthodes de la géométrie synthétique.
Ces cinq espèces sont :
- le tétraèdre régulier ;
- le cube ;
- l’octaèdre ;
- le dodécaèdre à douze faces ;
- l’icosaèdre à vingt faces.
(1), (3) et (5) ont pour faces des triangles équilatéraux égaux ; les faces du dodécaèdre sont des pentagones réguliers égaux. Pacioli a construit une preuve de ce théorème dans ses Proportions divines (Divine Proportione, 1494).
Une preuve plus rigoureuse a été donnée par Leonhard Euler (1707-1783), preuve qui est au centre du développement par Euler de la topologie sur la base de l’analysis situs de Leibniz.
On prouve facilement que chacun des quatre autres solides platoniciens est dérivé du dodécaèdre ; à ce propos, on montre également que la Section d’Or, méthode géométrique synthétique employée pour la construction d’un pentagone régulier ou d’un dodécaèdre, est le trait caractéristique de l’unicité des cinq solides platoniciens.
La conception de l’Acropole d’Athènes est l’éclatante démonstration du fait que les contemporains de Platon et ses prédécesseurs de la Grèce Classique utilisaient une géométrie synthétique construite à partir de la Section d’Or.
Aussi, en comparant l’œuvre d’Albrecht Dürer avec les rapports harmoniques employés pour la conception de l’Acropole, on peut montrer que les Grecs classiques comprenaient le principe redécouvert par Pacioli et Léonard de Vinci suivant lequel tous les processus vivants se distinguent géométriquement des processus non vivants par le fait essentiel que la morphologie de la croissance des processus vivants et des fonctions déterminées par cette croissance est celle d’un modèle soi-similaire de croissance, tel que la soi-similarité est dans un rapport harmonique congruent avec la Section d’Or.
Reconnaissons que, pour ces raisons, diverses sectes ont tenté de lire de mystérieuses propriétés dans le Pentagone et la Section d’Or. Il n’y a rien de mystique dans tout cela, pour quelqu’un qui connaît l’œuvre de Gauss et de Riemann s’y rapportant. Avant d’arriver au terme de ce texte, le lecteur, libéré de toute mystification, aura compris les rudiments de ce sujet et leur indispensable fonction dans la science économique. Pour les besoins de ce chapitre, il nous suffira d’effleurer ici quelques points directement à l’origine des découvertes de Leibniz en science économique.
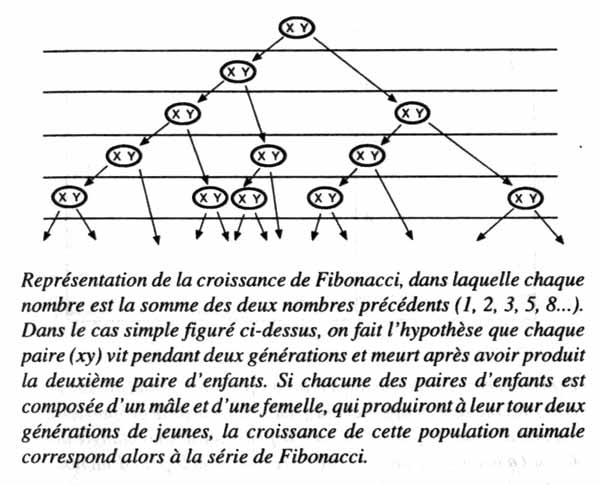
Premièrement, la signification de la relation de la Section d’Or à la morphologie des processus vivants commence à prendre sens une fois que l’on a reconnu pourquoi ce que l’on appelle une série de Fibonacci (Léonard de Pise, probablement âgé de 30 ans environ, quand il écrit son Liber Abaci en 1202) converge vers une valeur déterminée par la Section d’Or.
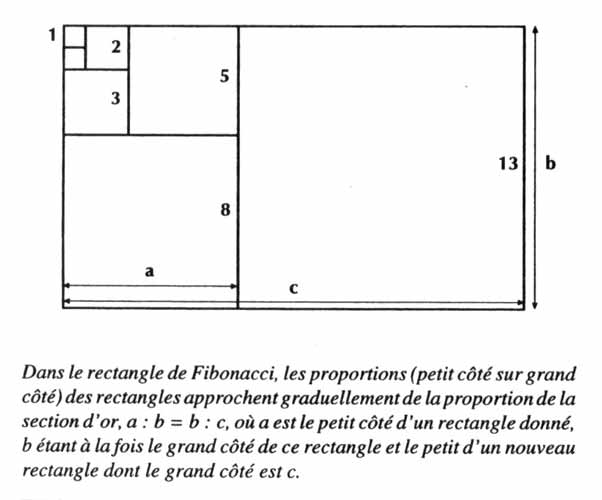
Une série de Fibonacci est une série géométrique (série de nombres entiers déterminés géométriquement) qui estime avec précision la croissance des populations, y compris celle des populations de cellules. Quand les nombres dans la série deviennent modérément grands, le rapport de deux nombres successifs dans la série converge rapidement vers la valeur de la Section d’Or. Avec une simple observation des plantes, on peut ainsi retrouver la découverte de Pacioli et de Vinci en ce qui concerne la vie végétale. Les travaux de Léonard sur l’anatomie des hommes, des chevaux, et d’autres organismes vivants consistaient principalement en une étude scientifique du même principe de la Section d’Or [7]. Non seulement les formes du corps humain, par exemple, sont déterminées par le principe de la Section d’Or, mais la dynamique de la morphologie des fonctions corporelles aussi.
Parmi les nombreuses branches de la science moderne fondées par lui, principalement sur la base de ces principes géométriques, Léonard de Vinci a appliqué ses études de la dynamique anatomique à la conception des armes, des outils et des machines. En ce qui concerne les armes, par exemple, la connaissance de la dynamique de l’anatomie a été utilisée pour les concevoir et les développer, comme s’il s’agissait d’outils, en tirant avantage des potentialités optimales des mouvements vigoureux du corps du combattant, de manière à ce qu’il porte le plus efficacement possible l’attaque contre l’adversaire en le mutilant ou en le tuant. C’est en partant du même point de vue, qu’il a développé les principes de la conception de machines.
Pour la simple conception des machines actionnées mécaniquement, on étudie les mouvements de l’ouvrier fabriquant un type de produit. L’observateur en déduit quels aspects de ces mouvements sont essentiels au travail effectué. Ces mouvements essentiels sont incorporés dans une machine à laquelle on fournit de l’énergie : énergie animale, énergie hydraulique, énergie éolienne, énergie calorifique... Ainsi, l’ouvrier utilisant cette machine a un plus grand pouvoir de production que le même ouvrier sans la machine.
Cependant, en général, la puissance appliquée au travail par une machine n’est pas la même que celle fournie à la machine en tant que telle. Une machine très simple, une lame de couteau, illustre ce point : la pression exercée par l’arête aiguisée de la lame est bien supérieure à la pression exercée sur le manche du couteau. La puissance est davantage concentrée. Nous mesurons une telle concentration de puissance comme accroissement de la densité du flux énergétique. Ceci mesure la concentration de puissance par centimètre de mouvement ou par mètre carré de la section d’action ou par mètre cube du volume d’action. Si on imprime une impulsion instantanée d’une tonne-poids à une machine, et si cette poussée est concentrée mille fois sur une surface de travail donné, on applique une impulsion instantanée à cette surface de travail au maximum égale à mille tonnes-poids. Dans notre texte, nous mesurerons fréquemment notre flux énergétique en kilowatts et notre densité de flux énergétique en kilowatts par kilomètre carré ou par mètre carré.
La première mesure des effets de la conception de machines est la comparaison entre l’effort humain requis pour faire fonctionner la machine, et la quantité de travail fournie par l’opérateur employant la machine. Si la machine est actionnée par autre chose que l’effort musculaire humain, nous devons mesurer le coût de production de l’énergie animale, de l’énergie hydraulique, de l’énergie éolienne ou de l’énergie calorifique en considérant l’effort humain consenti par la société pour s’organiser et fournir cette énergie à la machine. Nous pouvons le considérer comme le coût en capital nécessaire à la fourniture de cette énergie. Nous devons ensuite comparer les variations du coût en capital par opérateur utilisant telle ou telle classe particulière de machines avec les variations de son débit correspondant à cette utilisation.
Cette comparaison conduit à une fonction mathématique. Imaginez un graphe sur lequel on porte en ordonnées l’accroissement du débit de production par opérateur et en abscisses l’accroissement du coût en capital de l’énergie à fournir par opérateur. Maintenant, étendez le champ de cette fonction mathématique en ajoutant un axe des Z. Sur celui-ci, on porte l’accroissement de la densité du flux énergétique correspondant à l’effort consenti par la machine. Jusqu’à la fin du livre, nos références à une fonction mathématique de ce type désigneront la fonction tridimensionnelle identifiée ici.
Dans la transmission au travail, à travers la machine, de la puissance fournie à son entrée, une partie de cette puissance est perdue sous forme de « chaleur » ou autre. Le taux de perte est particulièrement intéressant quand nous accroissons significativement la concentration de puissance, la densité du flux énergétique de l’effort appliqué au travail. Nous rencontrons à ce point une considération curieuse, amusante. Nous tendons à accomplir de bien plus grands débits de travail avec une fraction de la puissance fournie à la machine à un niveau élevé de densité de flux énergétique, qu’avec toute la puissance fournie à la machine à un niveau de densité de flux énergétique relativement moins élevé. Il apparaît ainsi que moins de puissance accomplit plus de travail qu’une plus grande quantité de puissance : c’est là l’un des aspects curieux de la science économique qui touche plus ou moins directement à ses fondements.
L’autre aspect général de la fonction mathématique qui nous intéresse au plus haut point est le phénomène de la « diminution des taux de retour sur investissements ». A partir de quel moment les accroissements du coût en capital par opérateur, ou de la densité de flux énergétique ne nous permettent-ils plus le même taux de croissance de la production que lors des précédentes augmentations de l’intensité du coût en capital, ou de la densité du flux énergétique, ou des deux combinées ?
Les mêmes principes s’appliquent à l’agriculture. Nous mesurons la production de l’agriculture de deux manières :
1. la production par tête ;
2. la production par hectare ou par kilomètre carré.
En première approximation, nous mesurons la production elle-même en termes tels que boisseaux de blé, tonnes de production animale comestible... Finalement, en économie, nous devons mesurer ces produits comme des composants d’un « panier de biens ». Il y a deux « paniers » :
1. les biens d’équipement par opérateur employé dans l’agriculture, l’industrie, la construction, l’industrie minière et les transports ;
2. les biens de consommation exigés par tête pour l’entretien des ménages.
En utilisant les « paniers de biens » comme étalons de mesure, la production se trouve comparée aux apports nécessaires à la société qui effectue cette production. La production doit être mise en corrélation avec le nombre total de kilomètres carré occupés par cette société ; c’est une mesure du taux d’activité productive par kilomètre carré, une mesure associée à la notion de densité du flux énergétique. Les deux mesures, par kilomètre carré et par tête (par opérateur) sont combinées par le biais de la densité démographique.
Le cas de l’agriculture illustre la manière dont les principes déterminant la conception des machines à combustion s’appliquent à l’ensemble des processus économiques.
L’importance de la machine à combustion, dans le processus économique pris dans son ensemble, est mesurée à l’aune de l’économie d’effort humain total (et moyen). L’image de cette mesure est transmise par l’idée de fournir le même panier de biens par tête à l’aide d’un moindre effort de la société tout entière, et par le fait que le contenu de ce panier puisse être élargi, en quantité et en qualité, sans accroître l’effort engagé à cet effet par la société. Autrement dit, les méthodes d’économie du travail constituent l’essentiel du résultat à mesurer en économie politique. C’est le meilleur étalon pour mesurer le revenu national dans la comptabilité publique [8].
Nous avons déjà rapporté que l’utilisation générale de la combustion du charbon pour faire fonctionner les machines — en vue de supprimer la dépendance vis-à -vis de la combustion du bois ou de la puissance hydraulique ou éolienne — a été le critère adopté par Leibniz pour fonder la science économique. Nous avons déjà identifié les principales caractéristiques de la fonction mathématique exigée. Le coût de la production du charbon doit être comparé au bénéfice obtenu en brûlant le charbon pour faire fonctionner les machines. La fonction de la machine à vapeur, selon Leibniz, est de permettre à un opérateur utilisant cette machine, de parvenir à une production de travail égale à celle « d’une centaine d’autres » opérateurs ne disposant pas d’une telle machine. L’économie de travail (travail épargné) représentée doit être comparée au prix de la machine et à celui de la consommation de charbon. Le prix de la consommation de charbon inclut celui de son extraction minière et son transport de, ainsi que les coûts de la combustion requise pour le transformer en une source d’énergie pour la machine.
Dans notre description initiale de la fonction mathématique requise, donnée quelques paragraphes plus haut, nous avons défini la fonction dans les termes de référence appropriés à la comparaison de machines entre elles. Nous devons maintenant redéfinir cette fonction. Posons d’abord A, l’économie de travail obtenue par les améliorations des pouvoirs producteurs du travail apportées par les machines à combustion, et posons ensuite B, les coûts additionnels encourus par la société pour la production, la maintenance et l’entraînement de ces machines ; c’est la valeur de (A - B = C) ramenée par tête, C désignant la marge nette du gain de la société, qui doit être considérée dans la définition des termes portés sur l’axe des ordonnées. Ce gain C définit un nouveau niveau de production (et de consommation) par tête de la société, impliquant un élargissement du panier de biens estimé par tête. A quels niveaux d’augmentation d’intensité capitalistique et de densité du flux énergétique cette fonction indique-t-elle des retours sur investissements « en diminution » ?
On obtient la valeur approximative de l’intensité capitalistique en établissant le rapport entre travail total consommé (par opérateur de machine), en tant que capital, et travail moyen de l’opérateur sur la machine. Les coûts en capital à retenir pour établir ce rapport comprennent le travail requis pour produire et maintenir la machine, pour lui fournir son énergie, mais pas les postes constituants des « frais généraux » comme l’administration, les divers types de services non-scientifiques, les coûts de vente, les charges financières, etc.
Lorsque l’intensité capitalistique augmente, quel est le taux correspondant d’accroissement de la productivité moyenne du travail dans la société toute entière ? Nous pouvons encore prendre pour base de comparaison l’accroissement des pouvoirs producteurs de cette seule composante de la force de travail totale que sont les opérateurs actifs. En fait, ces deux mesures de l’accroissement de la productivité par tête devraient se recouper.
La « courbe » de notre fonction mathématique, définie par la mise en corrélation des accroissements de l’intensité capitalistique avec ceux de la productivité moyenne du travail, est une courbe décrivant l’accroissement de la capacité à accomplir du travail. Nous devons procéder à la même extension de cette fonction que celle à laquelle nous avons procédé pour définir le fonctionnement de la machine quelques paragraphes plus haut ; nous devons ajouter l’axe des Z, l’accroissement de la densité de flux énergétique. Nous obtenons alors une « courbe » qui décrit la diminution des retours sur investissements à partir d’un certain point d’accroissement de l’intensité capitalistique, si la densité de flux énergétique demeure constante. Nous obtenons aussi une courbe qui rentre dans une région de retours sur investissements en diminution si la densité de flux énergétique augmente à intensité capitalistique constante. Nous obtenons une courbe différente quand les deux s’accroissent simultanément. Les courbes intéressantes sont celles pour lesquelles l’intensité capitalistique et la densité de flux énergétique augmentent simultanément, mais avec des taux d’accroissement différents. Les plus intéressantes parmi celles-ci sont celles pour lesquelles les taux d’accroissement relatifs de chacune d’entre elles varient, linéairement ou non, et pour lesquelles les taux de variation de l’accroissement relatif des deux sont eux-mêmes décrits par une fonction mathématique. Cette fonction est une fonction du niveau d’intensité capitalistique et de la densité du flux énergétique.
En d’autres termes, dans les cas les plus intéressants, il est impossible de faire progresser efficacement l’intensité capitalistique sans agir, en même temps et aussi peu que ce soit sur la densité du flux énergétique. Il est impossible d’accroître efficacement la densité du flux énergétique sans agir un minimum sur l’intensité capitalistique. Ce cas intéressant est celui que l’on rencontre dans les processus économiques réels.
Imaginez le cas hypothétique de deux machines à combustion consommant la même quantité horaire d’énergie générée à partir du charbon, mais dans lequel un opérateur utilisant un de ces deux types de machines a un taux de production supérieur à celui d’un autre opérateur utilisant l’autre type. La différence entre ces deux types de machines est une différence tenant à l’organisation interne des machines. C’est sur cette différence que repose la définition donnée par Leibniz de la technologie (historiquement connue, en France, sous le nom de « polytechnique »).
L’économie physique est l’étude des types indiqués des fonctions mathématiques du point de vue de la polytechnique (ou technologie).
En première approximation, la polytechnique (ou technologie) est définie par la quantité équivalente d’action circulaire nécessaire à la transformation par la machine de la puissance appliquée en travail.
Comme en astronomie, par exemple, les processus internes de la machine sont étudiés en tant que cycles d’évolutions dans la direction de l’action appliquée, et tout cycle correspondant à ce changement est défini en englobant les moindres cycles. Avec l’aide de ce que Nicolas de Cues appelait le principe du minimum-maximum, le principe isopérimétrique, on détermine l’action circulaire équivalente à l’action accomplie par la machine. Ceci est l’application du principe de moindre action à l’analyse de la polytechnique (« technologie ») du cycle de la machine.
Ce n’est pas parce que beaucoup de machines sont associées à l’action de rotation que l’on adopte cette façon de faire ; les machines sont dominées par l’action rotative car cela est requis par le principe physique de la nature correspondant au principe de moindre action de Leibniz.
Pour ajouter la fonction de l’axe des Z de notre fonction mathématique générale, nous devons refléter l’accroissement de la densité du flux énergétique au sein de l’interprétation par l’action circulaire. Ceci conduit à un ordre supérieur d’action circulaire, l’action conique spirale. Les implications les plus profondes de ce résultat sont clarifiées en examinant cette caractéristique de la fonction à partir des remarquables travaux effectués par Gauss et Riemann sur les fonctions coniques spirales soi-similaires.
Il faut reconnaître qu’aucune institution dans le monde, en dehors de l’auteur et de ses collaborateurs, ne pratique aujourd’hui la science économique telle que Leibniz l’a définie ; en dehors des cercles entourant l’auteur, aucune université quelconque, à notre connaissance, ne traite la science économique comme Economie Physique, ou ne reconnaît que l’Economie Physique et la Physique Mathématique, se recoupent et constituent des sujets de recherche inséparables. A la suite du Congrès de Vienne de 1815, aucun nouveau travail dans le domaine de l’Economie Physique n’a été effectué. En dehors des programmes caméralistes établis ou poursuivis sous l’influence de Leibniz, le principal centre pratiquant l’Economie Physique au début du XIXe siècle a été l’Ecole Polytechnique de 1794 à 1815, sous la direction de Lazare Carnot et de son professeur Gaspard Monge. A partir de 1816, avec l’exil de Carnot en Allemagne, l’institution a été reprise et ruinée par Pierre-Simon Laplace (1749-1827), une destruction épistémologique et morale poursuivie sous la direction d’Augustin Cauchy (1789-1857) [9].
L’application des principes de l’Economie Physique aux progrès de l’économie politique fut poursuivie avec succès au-delà de 1815 par les représentants du Système Américain d’Economie Politique tels que Friedrich List (1789-1846), Henry C. Carey (1793-1879) et E. Peshine Smith (1814-1882). Carey, avec Henry Clay, fut un dirigeant des Whigs et le conseiller en économie du Président Abraham Lincoln. L’ami de Carey, E. Peshine Smith, fut, à partir de 1872, le conseiller de la Restauration Meïji au Japon, et a assisté le Japon dans sa marche vers une industrialisation aujourd’hui admirée et enviée dans maintes parties du monde. Ainsi, leur travail a eu un impact majeur sur l’histoire mondiale durant et au-delà de leur vie, mais ils n’ont apporté qu’une contribution marginale au corps des connaissances de la science économique telle qu’elle fut développée par Leibniz et ses successeurs de 1671 à 1815.
La méthode et le courant de Leibniz ont été par ailleurs vigoureusement maintenus en Allemagne par quelques institutions phare jusqu’à la mort de Gauss (1855), de son successeur immédiat, Lejeune-Dirichlet (1859) et du collaborateur et successeur de Gauss et Dirichlet, Riemann (1866). Bien que Dirichlet, un protégé de Alexander von Humboldt, ait étudié à l’Ecole Polytechnique en collaboration avec Humboldt et que Humboldt lui-même ait été en relation étroite avec Carnot jusqu’à la mort de ce dernier en 1823, le cercle de Humboldt à l’Université de Berlin et leurs alliés Gauss et les cercles de Göttingen n’ont pas étendu leurs remarquables découvertes en physique mathématique au domaine de l’Economie Physique en tant que telle. Il est singulier que l’auteur ait dû être le premier à reconnaître, en 1952, l’adéquation de l’œuvre de Riemann aux problèmes fondamentaux non encore résolus de la science économique.
Henry C. Carey était au moins quelque peu conscient de ce problème et de sa signification. L’Unité de la Loi de Carey (1872) est de ce point de vue exemplaire. Dans les grandes lignes, l’objectif de Carey est correct et nombre de ses arguments relèvent de conceptions qu’aucun étudiant sérieux en économie ne devrait négliger. L’aspect malheureux de ce livre réside dans le fait que Carey était à cette époque sous l’emprise d’une admiration déplacée pour le Professeur Eugen Dühring [10] de l’Université de Göttingen, une célébrité éphémère de l’époque. Sous cette influence, les références de Carey aux principes physiques reflètent l’autorité de personnalités et de thèses directement opposées à celles de Riemann et de Gauss. Aussi, bien que Carey insiste correctement sur la nécessité de la prise en compte de la thermodynamique en science économique, il s’appuie sur la mauvaise doctrine de la thermodynamique.
Les propres contributions de l’auteur à la science économique sont centrées sur une découverte faite d’abord en 1952. Dans le fil de son effort, pour réfuter la thèse de la « théorie de l’information » de Wiener-Shannon, il fut amené (au cours de la période 1948-1952), à étudier les travaux que Georg Cantor avait effectué sur les ordonnancements transfinis au cours de la période 1871-1883. Ceci le conduisit à corriger et à renouveler sa perspective sur les travaux effectués par Riemann dans la période 1852-1859 [11]. Il reconnut alors que la physique mathématique riemannienne résout implicitement le problème de la mesure de la relation existant entre une certaine quantité de progrès technologique et l’accroissement du taux de croissance économique en résultant. Aussi, la méthode développée à partir de ce point de départ est ici appelée méthode LaRouche-Riemann.
Nombre de mathématiciens et autres spécialistes de physique mathématique, ainsi que de disciplines associées, se sont joints aux étudiants des classes de science économique de l’auteur. Avec leur collaboration, à partir de 1970, la forme originale de la méthode LaRouche-Riemann a été développée et appliquée à l’analyse et aux prévisions économiques. Ce travail en science économique est inséparable des travaux qui se poursuivent sur la fusion thermonucléaire contrôlée et sur d’autres secteurs-frontières de la physique des plasmas. Dans cette mesure, la tradition de Leibniz et de l’Ecole Polytechnique put renaître.
L’importance d’un tel recouvrement d’activité est illustrée par les faits suivants.
Supposons que, dans certains cas, nous perdions 80% de la puissance fournie à une machine, ou à un processus, dans le cadre d’un effort visant à accroître la densité du flux énergétique de plusieurs ordres de grandeur ou plus encore. Cependant, dans quelques uns de ces cas, nous accomplissons plus de travail qu’il ne pourrait en être obtenu en utilisant 100% de la puissance fournie à des niveaux moins élevés de densité de flux énergétique. Nous avons souligné plus haut ce curieux phénomène : la simple conversion d’énergie en travail est une notion fallacieuse. Ce curieux phénomène est la caractéristique centrale des processus vivants, mais nous le rencontrons aussi en considérant d’autres aspects du travail scientifique.
Comme nous le démontrerons plus loin, la science économique considérée du point de vue de la physique mathématique riemannienne nous oblige à définir les termes de travail et d’énergie d’une certaine manière, une manière opposée à celle que Clausius (1822-1888), Helmholtz (1821-1894), Maxwell (1831-1879) et Boltzmann (1844-1906) ont popularisée. Pour des raisons établies avec certitude par Kepler, et par les compléments apportés par Gauss aux travaux de Kepler s’y rapportant, les notions de travail et d’énergie dérivées de la science économique sont nécessairement celles qui sont correctes, et se trouvent en conformité avec les notions de la physique mathématique riemannienne en tant que physique. L’économiste scientifique est par conséquent obligé de rechercher dans les travaux des physiciens et des biologistes les cas expérimentaux exigeant le recours aux mêmes notions de travail et d’énergie, que celles relevant de l’économie. L’objet principal de telles recherches est de dégager les aspects des processus physiques qui sont par nature les plus féconds pour le progrès de la technologie.