[sommaire]
Introduction
Par Pierre Bonnefoy,
auteur du livre Principes non-mathématiques de la Science (2020)
Lorsqu’il rédige ce texte en octobre 1994, le penseur et économiste américain Lyndon LaRouche (1922-2019) est sorti depuis peu d’un emprisonnement de cinq ans ordonné sous Georges Bush senior.
(Page spéciale centenaire de l’anniversaire de LaRouche.)
Entre-temps, l’Empire soviétique s’est effondré, comme il l’avait anticipé publiquement, mais l’espoir de voir s’instaurer une période de prospérité mutuelle entre les anciens ennemis de la Guerre Froide est trahi par l’Occident. L’illusion est entretenue à l’Est comme à l’Ouest, que le règne universel d’une économie de marché basée sur des modèles mathématiques statistiques, sera désormais « la fin de l’histoire ».
Mais ces modèles servent surtout à faire des algorithmes pour spéculer au détriment de l’économie réelle. Or, du fait que ce système néolibéral ne peut pas tenir compte, dans sa théorie, de la seule source réelle de richesse que constitue la créativité humaine, il est voué à s’effondrer à son tour dans une série de chocs de plus en plus violents, comme on l’a effectivement constaté depuis.
En 1994, personne ne veut voir le cancer spéculatif qui ronge l’économie réelle.
L’une des principales raisons de cet aveuglement collectif qu’identifie LaRouche, c’est la confusion qui règne dans tous les domaines de la science – en particulier dans l’économie, mais pas seulement – entre la réalité du monde physique et la modélisation mathématique.
Ce problème n’est pas nouveau : il se posait déjà sous une autre forme « néo-aristotélicienne » dans le domaine de la physique, à l’époque où l’algèbre de Descartes ainsi que l’empirisme de Galilée et de Newton venaient se substituer à la méthode platonicienne de l’hypothèse redécouverte à la Renaissance grâce au cardinal Nicolas de Cues, et mise en œuvre par Kepler. Comprendre cette bataille de l’histoire des sciences, donnerait un recul critique nécessaire par rapport aux théories économiques actuelles, à ceux qui cherchent une solution à la crise.
En 1994, Jean-Paul II qui avait contribué précédemment à la fin de l’Empire soviétique, s’oppose au malthusianisme récemment promu lors d’une conférence organisée au Caire par l’ONU contre la « surpopulation ».
Il faut préciser que depuis la « rencontre inter-religieuse d’Assise » organisée en 1986 par le président du WWF, le Prince Philip d’Édimbourg, une opération de subversion malthusienne est promue dans les grandes religions abrahamiques traditionnellement attachées au principe de la Genèse qui enjoint de « croître et multiplier ».
En dialogue sur cette question avec certains cercles du Vatican, LaRouche voit dans le malthusianisme une fraude scientifique destinée à empêcher le développement des pays pauvres pour en garder un contrôle colonial : un modèle mathématique qui postule que la quantité de ressources dont dispose notre société est une donnée fixe imposée par la nature, et non pas un produit de la créativité humaine. L’apartheid technologique imposé à ces pays dispose ainsi d’une « justification » apparemment scientifique.
Il est donc urgent à plus d’un titre de rétablir clairement la limite entre la véritable notion de science et les mathématiques.
Cependant, c’est également sous l’impulsion de Jean-Paul II voulant que l’Église ne refuse plus le progrès scientifique, que l’Académie pontificale des sciences reconnaît solennellement en 1992 l’injustice du jugement porté contre Galilée au XVIIe siècle.
Pour LaRouche, cela pose problème. Cela ne veut pas dire, bien entendu, qu’il approuve l’obscurantisme de l’Église à l’œuvre dans la persécution de Galilée ; mais tout le battage fait autour du procès de Galilée jusqu’à l’époque actuelle, laisse de côté une question épistémologique fondamentale concernant la méthode de découverte scientifique.
Il se trouve que celui qui a prouvé scientifiquement que la Terre « tourne », n’est pas Galilée mais Kepler qui, le premier, a donné une caractérisation de la raison physique de ce mouvement. Cette raison a pris par la suite le nom de « gravitation universelle ». Galilée a donné pour la trajectoire de la Terre un modèle mathématique basé sur le mouvement circulaire uniforme… donc faux dans le résultat mais également faux par son approche empiriste qui privilégie le modèle sans chercher la raison.
Le fait que depuis quatre siècles Galilée soit considéré comme une icône de la science, reflète la confusion d’esprit relevée par LaRouche au sujet des mathématiques et de la science.
Renouant avec l’esprit de la célèbre correspondance sur le transfini entre le grand mathématicien allemand Georg Cantor et le cardinal Franzelin à la fin du XIXe siècle, « La fraude de la causalité algébrique » s’adresse, entre autres, à certains cercles de l’Église pas toujours conscients du problème que leur pose l’hégémonie de l’aristotélisme, depuis l’Empire romain, dans leurs institutions.
Mais ce texte s’adresse également à certains cercles scientifiques qui, finalement, sont pollués par une idéologie très similaire. Il vise plus généralement à réhabiliter la science dont le véritable fondement ne se trouve pas chez Aristote mais chez Platon. Cet effort reste d’autant plus d’actualité que 25 ans après sa rédaction, les peurs millénaristes entretenues par un écologisme malthusien pervertissent la science, la politique et l’actuel pontificat de François.
On dit que « Science sans conscience n’est que ruine de l’âme » mais sans la science, pourrait-il encore y avoir une conscience ?
La fraude de la causalité algébrique [1]
Lyndon LaRouche, le 3 octobre 1994.
La distinction que Newton établit entre lois du mouvement ou axiomes d’une part, et hypothèses d’autre part, ne me semble pas défendable. La loi de l’inertie est l’hypothèse suivante : s’il existait, dans l’univers, quelque chose comme un point matériel isolé, et s’il venait à bouger à une vitesse déterminée, alors cette vitesse serait maintenue indéfiniment. (Berhard Riemann) [2]

Une fraude fondamentale a été introduite dans les mathématiques telles qu’elles sont en général enseignées aujourd’hui. On peut l’exposer succinctement en mentionnant le fait que la formule algébrique de l’attraction gravitationnelle de Galilée et de Newton découle directement de la troisième loi de Kepler, et qu’elle est donc, selon toutes les apparences formelles, parfaitement consistante, algébriquement, avec celle-ci.
Le point crucial de notre propos est le suivant. En dépit de cette consistance formelle, la notion de cause, essentielle dans la physique mathématique d’Aristote, de Galilée et de Newton, n’a pas d’existence ontologique dans la découverte originelle de ce principe de gravitation universelle par Kepler. En dépit de la consistance algébrique qui semble être le fondement même des deux calculs de la gravité, il existe, en termes de signification physique, une différence ontologique irréconciliable d’un point de vue axiomatique.
Cette différence axiomatique explique pourquoi Galilée et Newton utilisent une notion de réaction purement mécaniste, le terme « cause », là où Kepler utilise le terme « raison ».
L’examen de ce paradoxe nous amène directement au plus profond et persistant conflit de la physique mathématique telle qu’elle est enseignée depuis quatre siècles. Nous allons voir qu’il nous montre que l’origine du problème se trouve dans le fait que tous les aristotéliciens modernes, ainsi que les autres philosophes matérialistes [3], soit nient l’existence de la créativité, soit, comme René Descartes et Emmanuel Kant, relèguent son existence au domaine inintelligible de la superstition : que ce soit l’« intuitionnisme » kantien, ou dans la forme extrême héritée du culte orphique, un deus ex machina gnostique.
Abordons maintenant la question cruciale, à savoir le fait que Galilée a violé deux des principes les plus fondamentaux de la méthode scientifique utilisée par tous les grands découvreurs depuis deux millénaires.
Premièrement, Galilée viole le principe de rigueur scientifique établi par l’Ecole d’Athènes de Platon : principe par lequel Platon ainsi que ses étudiants et collaborateurs Eudoxe et Théétète ont démontré l’existence d’une classe de grandeurs appelée « incommensurable » qui ne peut dériver des nombres rationnels.
Deuxièmement, Galilée tombe dans le piège de l’« objectivité scientifique ». Il abandonne inconsidérément et imprudemment le principe fondamental de la méthode socratique de Platon selon lequel il ne saurait y avoir de méthode de connaissance de l’univers compétente qui ne rende compte, de manière adéquate, de l’existence de l’acte de découverte valide d’un nouveau principe par le savant. [4]
Ces deux erreurs de méthode, axiomatiques, fondamentales, commises par Galilée et Francis Bacon, les protégés de Paolo Sarpi, marquent tous les aspects spécifiques des travaux de Galilée, de Descartes et de Newton. Ce sont les fautes caractéristiques dont a hérité l’enseignement mathématique actuel. Dans les lignes qui suivent, l’examen de ces deux erreurs axiomatiques sera la base appropriée pour étudier le caractère fallacieux de la notion habituellement admise de « causalité ».
Les principes de la méthode scientifique
Dans toute l’histoire des sciences jusqu’à ce jour, la comparaison entre la notion de causalité de Kepler et celle de Galilée a posé implicitement trois types de questions axiomatiques :
- Les questions axiomatiques de méthode appartenant au domaine des mathématiques formelles (géométrie) ;
- Les questions axiomatiques de méthode platonicienne implicitement posées dans la célèbre thèse d’habilitation de Bernhard Riemann Sur les hypothèses qui servent de fondement à la géométrie (1854). [5]
- La question épistémologique à laquelle l’auteur de ces lignes a apporté une réponse du point de vue de l’économie physique, dans la période 1951-1952. [6]
Résumons-les successivement.
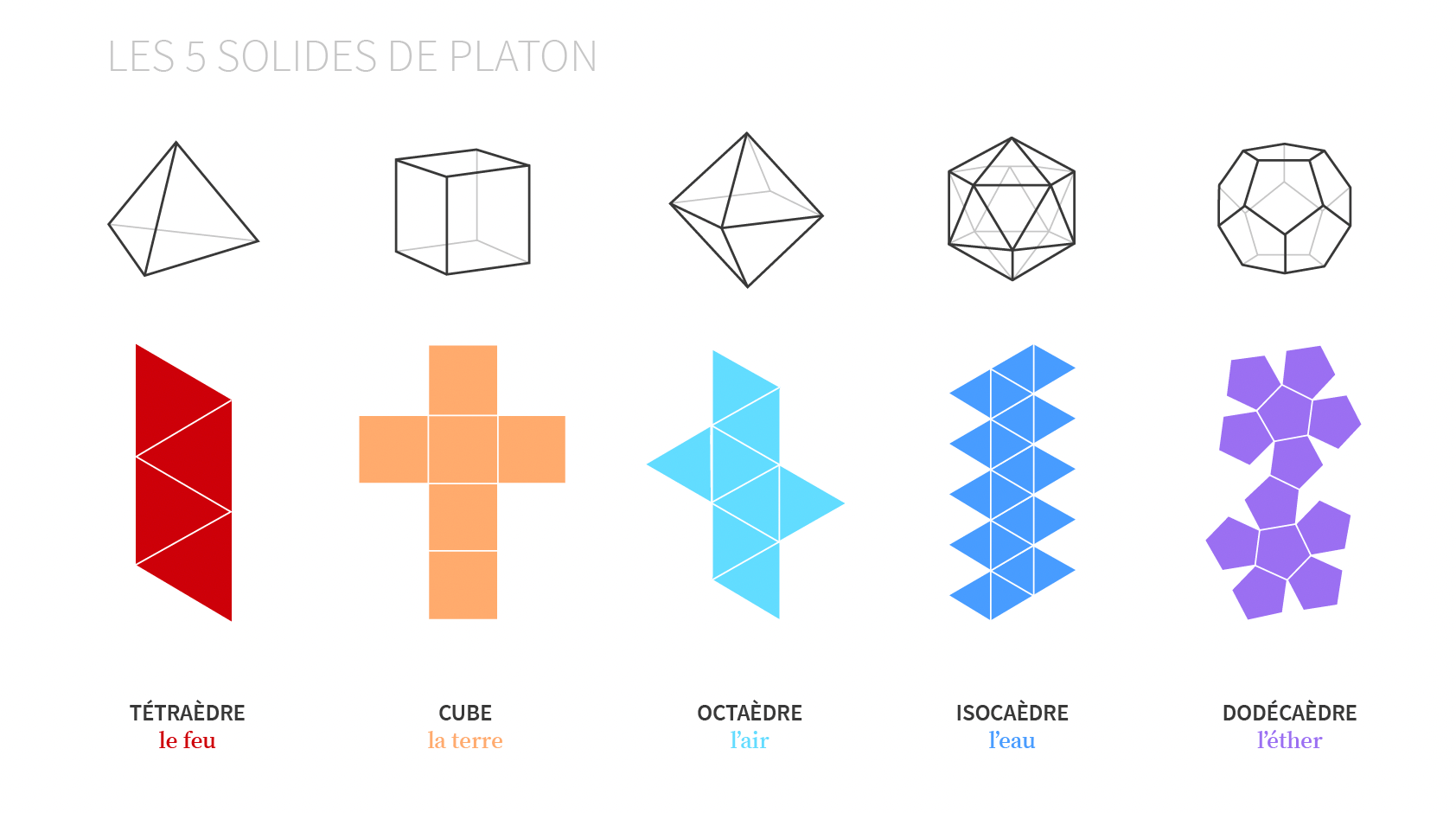
Commençons par illustrer les questions axiomatiques importantes de méthode formelle (c’est-à-dire mathématique) par deux exemples célèbres pris dans la géométrie grecque classique de l’Académie de Platon : d’abord, le cas de l’hypoténuse du triangle 3-4-5 et, ensuite, la détermination de la section d’or à partir de la construction d’une preuve de l’affirmation de Platon selon laquelle on ne peut construire que cinq solides réguliers qui soient circonscrits par la surface interne d’une enveloppe sphérique. [7]
Un triangle dont les côtés sont de proportions 3-4-5 est un triangle rectangle dont le côté le plus long est l’hypoténuse. La longueur de cette hypoténuse est-elle un nombre rationnel ou un nombre quadratique ? La réponse devient implicite lorsque nous reformulons la proposition de la façon suivante : du point de vue de l’algèbre, l’hypoténuse appartient à une classe générale de nombres |ai| qui sont égaux à :
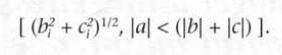
Elle appartient à une classe de grandeurs quadratiques que les classiques grecs incluaient parmi les « incommensurables ».
Cette réponse, si elle n’est pas tellement claire dans le cadre de la théorie moderne des nombres ou de l’algèbre [8], l’est pourtant parfaitement en géométrie.
Du point de vue de la méthode géométrique, deux grandeurs ne peuvent être dites « congruentes » sur la seule base du fait que leur accord semble coïncider dans les limites d’une marge d’erreur tolérable, mais seulement s’il existe une coïncidence inhérente dans la façon dont elles sont respectivement engendrées, tout comme en biologie l’on distingue les mammifères marsupiaux des placentaires. En d’autres termes, le signe « égal » de l’algèbre formelle et le signe « congruent » de la géométrie ne sont pas interchangeables.
Considérons maintenant notre deuxième exemple, tiré des mathématiques.
La valeur algébrique généralement calculée et citée pour la section d’or est environ le double du cosinus (le rapport des deux côtés) de l’angle aigu d’un triangle rectangle, dont l’hypoténuse est le côté d’un pentagone régulier. [9]
D’un point de vue superficiel, on pourrait considérer cette valeur comme exactement ou approximativement égale a celle obtenue pour la proportion d’or par le calcul algébrique. Cette erreur répandue ne tient pas tant à ce calcul lui-même mais au fait de supposer que ce nombre est un coefficient définissant les ordonnancements harmoniques que Luca Pacioli, Léonard de Vinci, et al., associaient aux processus vivants et que Kepler associait à la fois aux processus vivants et aux orbites des planètes. Cette erreur de supposition récurrente, commise de cette façon, constitue le paradigme du caractère fallacieux de la représentation algébrique de la causalité par Galilée et Newton.
Les solides platoniciens
Considérons ici la même question de principe posée par l’hypoténuse d’un triangle 3-4-5.
En mathématique (c’est-à-dire en géométrie), un phénomène est ce qu’il est engendré à devenir.
Comment Pacioli, Léonard de Vinci et Kepler engendrent-ils le pentagone à partir duquel est dérivé ce calcul de la grandeur de la section d’or ? Ils l’engendrent de la même façon que Platon.
Puisque les quatre autres solides réguliers de la série platonicienne découlent du dodécaèdre régulier, celui-ci constitue de façon unique la caractéristique d’un processus transfini de construction, par lequel on démontre que seulement cinq solides réguliers peuvent être inscrits dans la surface interne d’une enveloppe sphérique.
Puisque chacune des faces du dodécaèdre est un pentagone régulier, la section d’or tire sa signification du processus de construction géométrique par lequel on démontre l’unicité du dodécaèdre aux faces pentagonales.
Par conséquent, la détermination de la section d’or n’est pas seulement algébrique ; elle est plutôt le processus de construction par lequel on démontre l’unicité du dodécaèdre sphérique.
Ce n’est pas la valeur numérique de la section d’or qui définit l’ordonnancement harmonique auquel les processus vivants, les orbites planétaires, etc., sont associés.
En fait, ce comportement harmonique reflète le fait que nous existons dans un univers qui est délimité par une certaine courbure d’« espace-temps physique ». Les ordonnancements harmoniques des processus vivants, des orbites planétaires, etc., n’existent pas en fonction d’une certaine valeur algébrique donnée à la section d’or ; ils sont des reflets de la délimitation, de la « courbure » de l’« espace-temps physique » dans lequel nous existons.
Comme le Cusain, Pacioli, Léonard de Vinci et Kepler le soulignèrent après Platon, le domaine de la géométrie spatio-temporelle a certaines caractéristiques axiomatiques imposées de « l’extérieur » ne pouvant être expliquées que selon les termes du fait que cette géométrie (tout comme nous-mêmes) existe dans un « espace-temps physique » délimité par une courbure définie.
C’est la construction elle-même, par laquelle nous reconstruisons la conception de Platon de l’unicité des cinq solides platoniciens, qui définit la signification nécessaire de la section d’or ; celle-ci ne se trouve pas dans son approximation algébrique mais plutôt dans ses origines, c’est-à-dire comme membre d’un ensemble engendré de cette manière bien définie.
Ce principe méthodologique des mathématiques classiques est à la base de la notion développée par l’Académie d’Athènes, des grandeurs non rationnelles appelées « incommensurables ». Celles-ci incluent les grandeurs algébriques (euclidiennes), les non algébriques (transcendantes) et le transfini supérieur (c’est-à-dire les séries Aleph de Georg Cantor).
Elles sont classées ainsi selon leurs cardinalités relatives, ou puissances, de telle sorte que le type ayant une cardinalité supérieure subsume formellement tous les types ayant une cardinalité inférieure, alors qu’aucune des cardinalités relativement inférieures ne peut être rendue congruente à une supérieure. Dans le dernier type, les séries Aleph (dont la grandeur chaque terme est virtuellement sans dimension), seule la cardinalité relative est implicitement dénombrable : en première approximation, comme une série de puissances. Ainsi, il était déjà clair pour Nicolas de Cues, le premier découvreur de la valeur transcendante de ?, qu’aucun nombre algébrique ne pourrait jamais devenir congruent à ?. [10]
Cela nous conduit au double problème traité par la thèse de Bernhard Riemann sur les Hypothèses. [11] Le document parle de lui-même, nous allons donc nous limiter ici à en extraire les implications les plus pertinentes.
Géométrie et physique
L’appareil de perception humain nous représente le monde de l’expérience sensorielle, principalement en termes de vision et d’audition.
La géométrie d’Euclide est une tentative de codifier certains présupposés, ceux que nous serions tentés de faire à propos de la nature du champ visuel en soi, mais sans considérer de manière adéquate les implications ontologiques des développements physiques que nous pensons situer comme se déroulant à l’intérieur de ce champ visuel.
Par contre, l’étude de la parole et de l’audition montre que notre dispositif physique nous permettant de parler et d’écouter, nous présente un univers du langage vocalisé et du chant qui est ordonné selon des principes harmoniques incompatibles, entre autres, avec les suppositions axiomatiques naïves de la géométrie euclidienne. [12]
Platon est le premier dans l’histoire qui ait découvert une union intelligible entre les deux domaines, celui de la vision et celui de l’ordonnancement harmonique naturellement déterminé du langage vocalisé. Platon nous montre, en faisant référence aux cinq solides platoniciens, qu’il existe des ordonnancements harmoniques de phénomènes dans le champ visuel qui correspondent aux harmoniques de l’octave de la gamme bien tempérée, déterminés naturellement dans le domaine de l’audition.
Comme Riemann l’a souligné, il fut la première personne connue à avoir reformulé d’une toute nouvelle façon les implications de la conception de Platon, grâce à une découverte qu’il faite remonter au 1er mars 1853 et qui fut le sujet de sa thèse d’habilitation du 10 juin 1854. Cet écrit concis et soigneusement composé fait partie des exposés les plus lucides et les plus profonds de toute la littérature scientifique. Pourtant, dans leurs commentaires concernant ce sujet, presque toutes les autorités généralement reconnues firent des contorsions afin d’éluder certains éléments cruciaux apparaissant clairement dans le texte. Nous devons donc mettre de côté tout ce que ces autorités ont dit au sujet de cette thèse, y compris, par exemple, ce qu’en dit Albert Einstein ; prenons le texte original de Riemann et suivons ses propres termes.
Commençons, comme Riemann, par la représentation de l’espace et du temps par Euclide [13]
C’est une erreur naturelle que de tenter, au premier abord, d’imaginer le champ visuel comme s’étendant indéfiniment selon des lignes droites – vers l’avant, l’arrière, les côtés, le haut et le bas –, et les évènements se produisant en des points référencés au moyen de ces lignes droites. Il est dès lors inévitable que quand nous étudions des qualités de l’espace-temps physique telles que la masse, les réactions chimiques, etc., nous soyons tentés, en vain toutefois, de représenter les processus physiques comme un système d’évènements se produisant à l’intérieur d’un modèle euclidien d’espace-temps.
Nous devrions nous rendre compte qu’en tentant de représenter des processus physiques en termes d’espace-temps, nous ne faisons que représenter les ombres que la réalité des processus physiques projette sur notre image mentale du type d’« espace-temps vide » qui est le sujet des Eléments d’Euclide. Nous nous trouvons ainsi dans la caverne de Platon telle qu’elle est décrite dans sa République.
Existe-t-il donc un moyen nous permettant de surmonter les limites de ce cauchemar nominaliste – le fait que notre imagination visuelle dépende de ces ombres ? Dans l’ensemble de ses recherches concernant l’histoire des mathématiques, Riemann professe n’avoir découvert que trois indices sur la façon dont on pouvait surmonter ce problème de l’imagination visuelle. Deux de ces indices avaient été proposés par Carl Gauss qui reprenait les travaux réalisés par L’Académie de Platon dans cette même direction, pendant environ les deux siècles précédant l’an 200 av. J.C. Le troisième et dernier indice fut apporté par les propres réflexions de Riemann sur les travaux du philosophe anti-kantien Johann Friedrich Herbart. [14]
Sur ce troisième point, la perspicacité de Riemann, quoique cruciale, ne fit qu’indiquer la direction dans laquelle on pouvait trouver une solution ; celle-ci fut apportée pour la première fois par la découverte originale de l’auteur de ces lignes dans la période 1951-1952. [15]
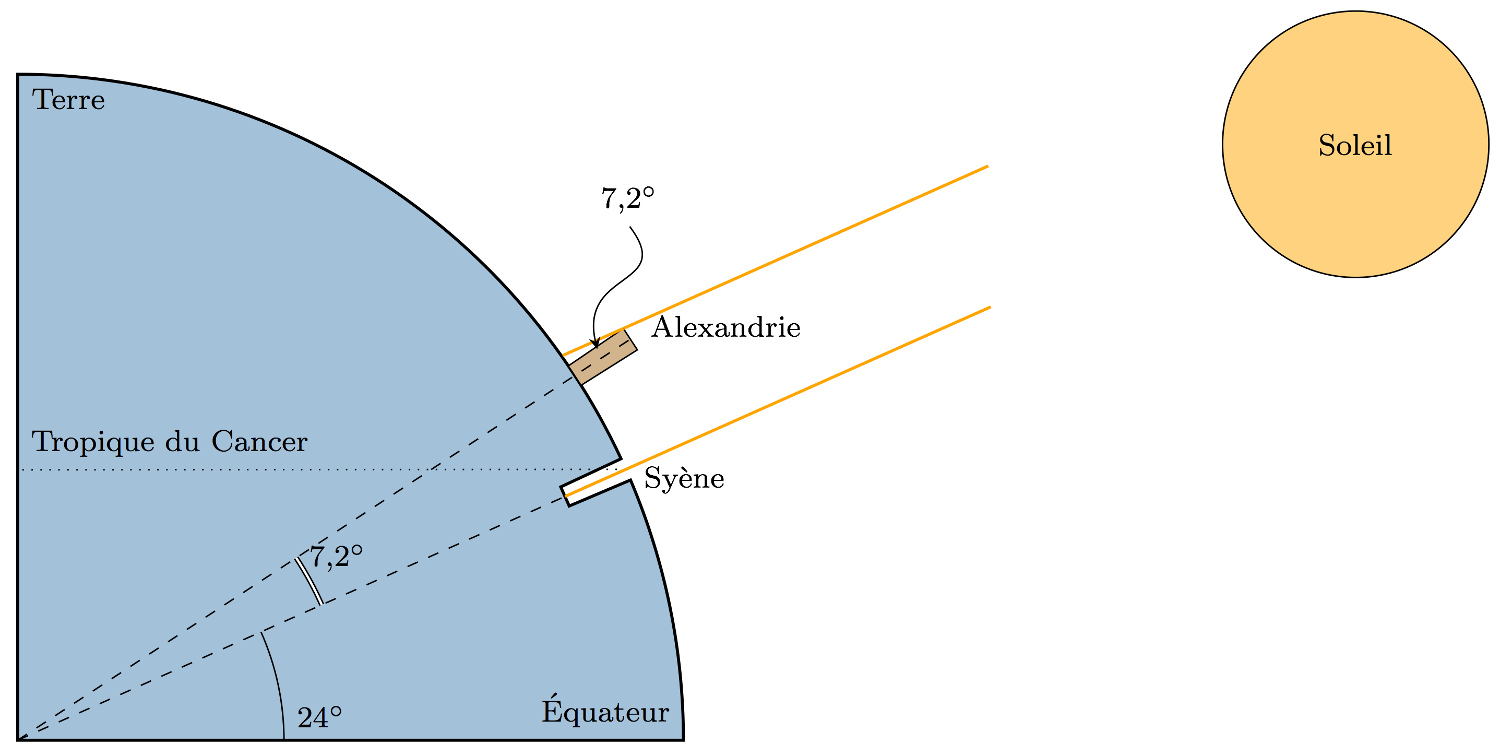
Remontons au IIIe siècle avant J.-C., lorsque le grand académicien Eratosthène mesura le diamètre terrestre avec une marge d’erreur de seulement 80 kilomètres. [16]
Par la même méthode, les Grecs mesurèrent de façon très satisfaisante [17] la distance de la Lune à la Terre et de la Terre au Soleil [18]
Nous devrions considérer ces accomplissements des mathématiques classiques grecques comme répondant aux paradoxes des ombres identifiés par Platon, et par la thèse d’habilitation de Riemann. Nous nous trouvons devant ce qui nous apparaît être la surface plate de la mer ou d’un lac par temps calme, et pourtant nous sommes capables de faire des mesures sur des ombres par lesquelles la réalité de la forme sphérique de notre planète et celle des distances à la Lune et au Soleil nous sont révélées.
Riemann lança le défi de faire la même chose, d’une façon plus générale et plus moderne : décoder les ombres que le monde physique projette sur notre imagination visuelle. En d’autres termes, appliquer à l’ensemble des phénomènes physiques les méthodes d’inférence employées en astronomie classique et en géodésie terrestre.
Environ deux mille ans après les Grecs, Carl Gauss avait amélioré leurs mesures astronomiques et géodésiques en affinant leur méthode par des mathématiques plus élégantes. C’est à la lumière de cette histoire que nous devons considérer l’importance que Riemann accordait à ces questions ; les travaux poussés de Gauss sur ces problèmes d’astronomie, de géodésie et de magnétisme terrestre apportent des indices pour résoudre les paradoxes des ombres de la perception sensorielle.
Les travaux de Riemann sur ce sujet peuvent être traités en deux phases fonctionnellement interdépendantes. Dans la première phase, on doit considérer les méthodes de mesure devant être appliquées à la géodésie du domaine paradoxal des ombres. On peut sans inconvénient caractériser cela comme le défi de mesurer la « courbure » de l’espace temps physique : reconstruire une image du processus physique à partir de l’étude du comportement (changement) de l’ombre que ce processus projette sur le monde des ombres qu’est l’espace-temps visuel et perceptif. Il est utile de nommer ce problème mathématique « la géodésie de l’espace-temps physique ».
Dans la seconde phase, nous considérons les « questions subjectives » que Riemann identifie sous la rubrique de ses critiques de l’œuvre d’Herbart : les moyens par lesquels l’esprit humain peut se rendre intelligible les méthodes de découvertes permettant d’accroître le pouvoir de l’humanité sur la nature par tête et par kilomètre carré.
Dans la seconde phase, en fait, nous nous posons la question paradoxale : « Qu’est-ce que le savoir humain ? »
Le moyen le plus facile et aussi le plus pertinent de comprendre les notions riemanniennes d’une géodésie générale de l’espace-temps physique, consiste sans doute à considérer la consistance algébrique apparente des formules que donnent Kepler et Newton de la loi de la gravité.
Etant donnée l’équation de Newton, demandons-nous quelle est la courbure de l’espace-temps physique dans laquelle cette formulation algébrique est applicable ? La réponse devrait nous sauter aux yeux ; en première approximation, la formule de Newton requiert un univers dont la courbure de l’espace-temps physique est déterminée par l’ensemble même de relations harmoniques que Kepler avait dérivé, dès le début, du traitement par Pacioli et Léonard de Vinci du principe des cinq solides platoniciens. Il faut voir cela dans la continuité des succès des classiques grecs, comme Eratosthène, qui découvrirent la géométrie du Système solaire en mesurant les ombres localement visibles sur la surface de la Terre.
Nous devons imaginer les caractéristiques essentielles de notre appareil de perception, la vision et l’audition, comme des écrans sur lesquels est projetée l’ombre de la réalité physique. Nous voyons alors les absurdités qui en résulteraient si nous tolérions le dogme nominaliste consistant à dépendre uniquement de nos perceptions sensorielles, comme le font les empiristes et les autres matérialistes (de même que les aristotéliciens d’une façon plus générale).
Par une cartographie « géodésique » appropriée des formes efficientes de relations (« actions ») entre les phénomènes physiques, nous déduisons une géométrie d’une courbure différente de la courbure zéro de l’espace-temps des euclidiens, de Galilée, de Descartes et de Newton. Le résultat que nous appelons « géométrie physique » ou « géométrie » de l’« espace-temps physique », est un espace différent de l’espace-temps de la simple perception, un « espace-temps physique » dont la « géométrie » n’est ni la géométrie linéaire (déductive) de la perception visuelle développée dans les Eléments d’Euclide ni les dogmes admis à tort par Galilée, Fludd, Bacon et Newton.
Ceci met davantage en relief le fait que la substance efficiente de la réalité physique n’existe pour l’homme que sous la forme d’une espèce d’idées qui ne font pas partie de celles que nous associons avec les perceptions sensorielles.
La notion de « courbure » riemannienne de l’« espace-temps physique » est le type d’idées que les philosophes vénitiens aristotéliciens et leurs étudiants, comme Pietro Pomponazzi, Francesco Zorzi (« Giorgi »), Paolo Sarpi, Francis Bacon, Galilée, Antonio Conti, Isaac Newton, Giammaria Ortes, lord Kelvin ainsi que tous les empiristes modernes et les positivistes, ont toujours voulu voir exclure du domaine de la science.
Voilà quelle était la raison des attaques de Paolo Sarpi, et de ses agents Fludd, Galilée et Francis Bacon, contre les travaux de Léonard de Vinci et Johannes Kepler. Voilà les raisons de la guerre que le vénitien Conti et ses créatures comme Voltaire, Giammaria Ortes, Francesco Algarotti, David Hume ou Leohnard Euler, le pion d’Algarotti, livrèrent contre la Théodicée et la Monadologie de Leibniz. [19]
Ceci est clef pour comprendre la différence irréconciliable entre la notion de causalité chez Galilée et Newton, et la notion toute différente de raison chez Platon, Nicolas de Cues, Léonard de Vinci et Johannes Kepler.
Passons maintenant au troisième indice de la thèse de Riemann qui renvoie à ses commentaires antérieurs sur l’œuvre de Herbart. Nous devons maintenant quitter le domaine préféré des empiristes aristotéliciens – celui de la pure perception sensorielle – pour entrer dans le domaine de ce que Platon définit comme « idées », Leibniz comme « monades », Riemann comme Geistesmassen, et le présent auteur comme « métaphores » ou « objets intellectifs ».
Le principe d’hypothèse supérieure
Les principes de la connaissance humaine ne doivent pas découler directement de ce que l’on appelle aujourd’hui la « physique mathématique », mais plutôt des formes classiques de poésie, de tragédie, de musique et des formes d’art plastique telles que les peintures de Léonard de Vinci et Raphaël. Cependant, il n’est pas seulement convenable mais également nécessaire aujourd’hui, de considérer comment la créativité se reflète dans le domaine du formalisme mathématique. Posons-nous la question suivante : comment les mathématiques formelles identifient-elles le véritable principe de métaphore tel qu’il se trouve dans la poésie, la tragédie et les formes classiques de composition musicale ?
Du point de vue des mathématiques formelles, par exemple d’une géométrie euclidienne, toute connaissance humaine apparaît comme étant le produit d’une combinaison de quatre niveaux – du plus bas au plus élevé – de méthodes intellectuelles de découverte.
Au plus bas niveau de développement de la connaissance humaine, nous trouvons la méthode de la logique formelle. Nous avons ici une liste extensible de théorèmes mutuellement consistants qui repose sur un ensemble commun fixe de propositions, semblable aux axiomes et postulats de la géométrie dite euclidienne (il n’est pas nécessaire d’expliquer ici pourquoi une telle organisation est quelquefois appelée un « réseau de théorèmes »). A ce niveau, la « découverte » s’exprime par la preuve de la consistance d’une certaine nouvelle proposition avec le système, preuve établissant cette proposition comme un théorème supplémentaire dans l’ensemble du réseau de théorèmes.
Après celui-ci, tous les niveaux supérieurs de découverte de nouveaux principes valides de connaissance se trouvent dans le domaine de l’hypothèse tel que défini par Platon.
Supposons quelque phénomène bien défini, comme une démonstration expérimentale, dont l’occurrence contredise la consistance d’un réseau de théorèmes existant. Ce résultat anormal, ou mieux, paradoxal, ne peut être résolu qu’en infirmant quelques-uns des axiomes et postulats interconnectés constituant dans leur ensemble le « principe générateur héréditaire » du réseau de théorèmes en question. Une fois la correction effectuée, le nouveau réseau de théorèmes défini par ce changement de « principe germinal héréditaire » doit être réconcilié avec les faits se rattachant aux anciens théorèmes précédemment établis du réseau de théorèmes rejeté. [20]
Cette révolution axiomatique validée, produisant un nouveau réseau de théorèmes supérieur à l’ancien, est une hypothèse simple.
Considérons ensuite la forme de découverte qui occupe le rang supérieur.
Pour illustrer la signification du terme hypothèse supérieure, référons-nous à la liste déjà citée des différents niveaux généraux de cardinalité (« puissance ») en mathématique. En réexaminant l’histoire interne des mathématiques du point de vue des ordonnancements du transfini supérieur de Cantor, on voit que la succession des changements axiomatiques révolutionnaires définissant la série des types de cardinalité mathématique rationnelle, algébrique, transcendante et Aleph est obtenue par une méthode constante de génération d’hypothèses. Dans les termes du Parménide de Platon, la conception de ce type de méthode constante de génération d’hypothèses est l’Un par rapport aux quatre Multiples (les quatre types de cardinalité). [21]
Au cours du temps, on a découvert des types valides d’améliorations dans les méthodes de génération d’hypothèses. Ces changements ne rendent pas les méthodes précédentes inutiles, mais ils introduisent plutôt de nouvelles dimensions de puissance et d’étendue à la capacité de découverte humaine. Platon identifie le principe dans lequel s’inscrivent ces progrès successifs de la qualité des hypothèses supérieures comme « faire l’hypothèse de l’hypothèse supérieure ». Ce principe (faire l’hypothèse de l’hypothèse supérieure) classe les hypothèses supérieures par ordre de cardinalité (puissance relative) ; ce principe est un Un par rapport au Multiple de la succession ordonnée d’hypothèses supérieures.
Il est nécessaire d’étendre ces notions au-delà de l’exemple mathématique ci-dessus, pour entrer dans le domaine supérieur de la « géométrie physique » – « l’espace-temps physique », le domaine de la physique qui est reflété sous forme d’ombres dans le champ de notre imagination visuelle, de notre vision mathématique.
Comme Platon le découvrit le premier, l’examen de la conditionnalité hypothétique d’une mathématique géométrique donnée, libère nos esprits de la marelle du formalisme logique et nous prépare à voir les mathématiques comme un outil permettant de cartographier la géodésie des ombres que l’espace-temps physique projette sur notre imagination visuelle.
Dans les salles de classe (et ailleurs), l’ineptie habituelle consiste à prétendre que l’expérience isolée est la base pour prouver les théorèmes. On y entend un argument pseudo scientifique, incompétent mais à la mode, selon lequel la preuve se trouverait dans la « reproductibilité » du phénomène. Or la fonction de telles expériences est au mieux négative : on ne prouve rien par le test expérimental isolé d’un théorème particulier ; en fait, le rôle des expériences est de nous aider plutôt à découvrir non seulement les erreurs communes, mais aussi, et c’est plus important, le genre d’anomalies qui créent des paradoxes dans l’ensemble de postulats utilisé pour la conception et l’interprétation de l’expérience, ou de l’observation, comme en astronomie.
La qualité de preuve pertinente ne peut se situer à un niveau de conceptualisation inférieur à celui de l’hypothèse supérieure. Un aperçu historique de l’économie physique nous en offre l’illustration la plus immédiatement accessible.
La seule preuve expérimentale de la légitimité d’un changement dans la méthode scientifique des formes de découvertes de révolution axiomatique, se trouve dans l’accroissement qui en résulterait pour la densité de population potentielle de l’espèce humaine. Ceci est statistiquement corrélé à des changements dans le niveau du progrès scientifique réalisé.
Une attention particulière doit être portée ici sur deux ensembles de faits aisément observables. Premièrement, les améliorations de l’espérance de vie, de la santé et de la démographie reproductive de la société, mesurées par tête, par ménage et par kilomètre carré. Deuxièmement, les améliorations de la puissance productrice du travail, également mesurées par tête, par ménage et par kilomètre carré. On met en regard ces deux ensembles de conditions observables avec la présence ou l’absence de changements culturels entraînés par l’application des découvertes considérées, sous forme de technologie. [22]
Il faut ajouter ici deux mises en garde. De même que l’autorité intellectuelle d’une découverte d’un nouveau théorème à l’intérieur d’un réseau de théorèmes dépend de sa consistance avec le principe axiomatique « héréditaire » de ce réseau de théorèmes, l’autorité d’une nouvelle hypothèse particulière dépend du type particulier d’hypothèse supérieure auquel cette nouvelle hypothèse appartient. Ainsi, l’autorité intellectuelle putative de toutes ces découvertes, d’une variété ou de l’autre, dépend de la validité du type d’hypothèse supérieure par laquelle elles sont subsumées.
Il nous faut donc insister sur le fait que chaque forme formaliste de réseau de théorèmes repose sur un ensemble spécifique de postulats axiomatiques interdépendants : le « principe héréditaire » sous-jacent au réseau. Chacun de ces principes est ainsi une hypothèse, une hypothèse qui est un élément individuel des « Multiples » hypothèses qui sont toutes et chacune subsumées (ou engendrées) par un type spécifique d’hypothèse supérieure.
Le concept d’hypothèse supérieure, quant à lui, est défini par la notion de faire l’hypothèse des hypothèses supérieures – le Un des Multiples hypothèses supérieures. Le Un – réseau de ces Multiples hypothèses supérieures – est ordonnancé par un principe de changement [23], le principe de changement manifesté comme l’ordonnancement des taux d’accroissement du potentiel de densité démographique relativement supérieurs lorsque l’on choisit une hypothèse supérieure plutôt qu’une autre.
C’est ici que la forme première d’existence – la véracité scientifique – est située à l’intérieur de la connaissance humaine. [24]
Par conséquent, la réaction à une action ne se produit pas conformément à quelque principe mécanique constant, elle ne suit pas la causalité que Galilée, Newton, et al., enferment dans la représentation mathématique des soi-disant « lois du mouvement ». Au contraire, la règle est que la réaction doit être conforme à quelque légitimité universelle, implicitement la loi de Dieu ou Raison.
Quelle est la forme de la loi de Dieu : ce serait un pur blasphème de suggérer que les lois de Dieu sont fixes dans le sens d’une méthode aristotélicienne prescrivant implicitement une liste fixe de « faites ceci » et « ne faites pas cela ».
Nous devons considérer la distinction que Platon fait entre le Devenir et le Bien ; il s’agit, dans les termes que Georg Cantor utilise à des fins pédagogiques utiles, des notions équivalentes de Transfini et d’Absolu.
La forme ultime du Devenir est une généralisation, en tant que Un, de la Transfinitude qui englobe toutes les hypothèses possibles de l’hypothèse supérieure : la notion implicite de ce principe universel et éternel de l’Intelligence créatrice supérieure dont le changement interne classe par ordre de puissance le Multiple, toutes les hypothèses supérieures possibles. Dieu le Créateur n’est rien moins que cela et sa pratique, sa loi ne peut être d’une moindre qualité que cela. Ceci – sa Loi – est la Raison. Ce qui se conforme à ce principe de changement connu comme étant l’hypothèse supérieure, est ce que Kepler et Leibniz entendent par raison.
Les implications physiques de cette distinction
Prenons, comme illustration de cette distinction, le cas du développement du principe universel de moindre action par Leibniz et Jean Bernoulli. [25]
Les travaux de Bernoulli sur la réfraction de la lumière dans un milieu de densité constamment croissante montrent la correspondance manifeste entre cette courbure et la courbure isochronique primaire, celle de la cycloïde. Ceci est un parfait exemple de mesure riemannienne de la courbure de l’espace-temps physique, une mesure effectuée dans les termes des ombres que l’univers réel projette sur le domaine de l’imagination visuelle.
Cette démonstration satisfit à la fois aux questions de « temps le plus court » (brachistochrone) et de « temps constant » (isochrone). Ceci montra, à la lumière des travaux antérieurs de Christiaan Huygens et d’Ole Römer [26], que les méthodes algébriques de Galilée, Descartes et Newton appliquées au mouvement devaient être remplacées par la géométrie supérieure du domaine transcendant.
Cette mention du cas de la brachistochrone suffit ici à notre dessein. Ce qu’il faut retenir ici, c’est la relation entre la notion leibnizienne de moindre contrainte [27] et l’utilisation par Kepler du terme raison là où les empiristes utilisent le terme cause.
Formellement, dans le sens où ce terme peut être attribué à Platon, Nicolas de Cues, Léonard de Vinci, Kepler ou Leibniz, raison signifie l’emploi rigoureux des facultés de découverte valide de principes coïncidant avec ce que j’ai appelé « hypothèse » ici et dans d’autres écrits.
Ce principe découvert a approximativement la force d’une estimation de la loi de Dieu (loi naturelle) à laquelle doit obéir l’impulsion à agir dans cet univers. Le principe de loi naturelle agit sur l’impulsion à agir comme une contrainte ; la soumission de l’impulsion à cette contrainte peut être vue comme analogue à la « soumission » de cette action conformément à ce qui apparaît à notre imagination visuelle comme une courbure de l’espace-temps physique. L’imagination d’une courbure des ombres de la réalité nous sert alors de représentation, d’une façon mathématique, de notre connaissance de la réalité ainsi reflétée.
Ainsi, nous trouvons parmi les prédécesseurs les plus importants de la thèse de 1854 de Riemann sur l’hypothèse, les travaux de Jean Bernoulli et de Leibniz qui, utilisant les caractéristiques du principe général de réfraction de la lumière, démontrèrent le principe leibnizien de la contrainte minimum universelle [28]
Le fait que la distance la plus courte dans le temps corresponde à un tracé isochronique, c’est-à-dire celui de la cycloïde primitive, suffit pour prouver que la vision elle-même n’est pas située à l’intérieur de l’espace algébrique des notions de causalité de Galilée et de Newton.
Leibniz, Bernoulli, et al., utilisèrent cette expérience cruciale pour discréditer l’attachement des cartésiens et des newtoniens aux méthodes algébriques et pour insister plutôt sur le domaine non algébrique (transcendant). Néanmoins, aussi justifiée et importante que fut (et que reste) cette correction, cela ne doit pas être interprété de façon à situer la causalité à l’intérieur du domaine transcendant plutôt que dans le domaine algébrique. N’oublions pas le moyen – la raison créatrice – par lequel on est monté du domaine algébrique au domaine transcendant : nous devons nous concentrer sur l’acte de découverte qui a permis le changement de révolution axiomatique vers un domaine mathématique de cardinalité supérieure. L’implication de ces deux considérations combinées – la question de la courbure et l’acte de sa découverte – est dévastatrice pour l’autorité suprême que revendiquent les « grands prêtres » des mathématiques généralement acceptées aujourd’hui.
Cela nous mène à la dernière étape de notre principal argument : l’importance ontologique de la preuve en économie du principe de l’hypothèse de l’hypothèse supérieure. Considérons d’abord les grandes lignes de cette preuve.
- La réalité ontologique de l’existence de toute découverte, que ce soit un nouveau théorème ou un nouveau principe de la nature (une hypothèse de qualité platonicienne), c’est la méthode employée pour engendrer cette découverte. La méthode de découverte d’un nouveau théorème consistant avec un réseau de théorèmes c’est l’hypothèse ; c’est également la méthode de découverte de ce réseau de théorèmes. Dans le cas d’une succession de réseaux de théorèmes ordonnés par classe de cardinalité (puissance) croissante, nous avons un réseau d’hypothèses, chacune étant ordonnée par rapport aux autres en termes de cardinalité, et toutes étant subsumées par une méthode constante de génération d’une telle succession d’hypothèses – une hypothèse supérieure.
- Dans les deux cas, toute nouvelle découverte pose la question de la véracité du savoir précédent. a) Dans le premier cas (le cas inférieur), celui du nouveau théorème valide d’un réseau de théorèmes, le savoir antérieur s’il est mesuré en termes de théorèmes, est entaché d’un raisonnement fallacieux ; néanmoins, le principe (l’hypothèse) soutenant communément la génération de tous les théorèmes valides de ce réseau, anciens comme nouveaux, est déclaré comme étant relativement véridique, transfinitivement véridique. b) Dans le deuxième cas de qualité supérieure, la découverte d’une nouvelle hypothèse remplace ce qu’affirmaient les hypothèses existant précédemment. Par rapport à la nouvelle, toutes les hypothèses précédentes sont entachées d’un raisonnement fallacieux. Néanmoins, la succession de telles découvertes, si des dernières sont d’un type transfini, est déclarée relativement véridique.
- Dans les deux cas, c’est le transfini relatif Un qui est relativement véritable, et chacun des termes des Multiples termes subsumés, pris en soi-même, est montré comme étant entaché d’un raisonnement fallacieux. Dans tous les cas, la vérité repose seulement sur le Devenir transfini, le type de principe de découverte de révolution axiomatique employé, plutôt que sur les faits expérimentaux associés au cas particulier. Ce type de principe de découverte (par exemple, l’hypothèse supérieure), plutôt qu’une hypothèse particulière, est toujours le lieu ontologique de véracité relative.
- Cela pose une question formelle, à savoir si la véracité relative de l’hypothèse supérieure n’est que la véracité de l’observateur (vérité de commentaire), ou si cette connaissance représente la véracité efficiente au sens ontologique ? S’il est montré que le principe de l’hypothèse supérieure employé correspond à quelque chose délimitant de l’extérieur le phénomène de changement dans les processus naturels, par exemple dans les lois apparentes du mouvement, alors cette correspondance montre que la véracité relative de la connaissance du principe est ontologiquement efficiente, et non simplement contemplative.
Le fait que le progrès technologique dans les puissances productives du travail entraîne un accroissement du potentiel de densité démographique de l’espèce humaine, en termes de consommation et de productivité par tête, par ménage et par kilomètre carré, reflète le processus de progrès scientifique inspiré des travaux de l’Académie de Platon et amorcé par la Renaissance à partir du milieu du XVe siècle. Le fait que cet accroissement dans les pouvoirs (re)producteurs de l’humanité soit en corrélation avec l’accroissement mesurable de la puissance (cardinalité) de la représentation géométrico-mathématique de la succession des découvertes employées, montre que le principe platonicien, anti-aristotélicien, de découverte créatrice sous-tendant la Renaissance et son héritage, est le critère pertinent de véracité ontologiquement valide. Cela montre également l’erreur relative des arguments utilisés par les Lumières et d’autres opposants à cette Renaissance.
Ce serait une erreur de croire que ce progrès a été uniquement ou même presque entièrement le résultat de progrès dans ce que l’on appelle les sciences naturelles. Ce que nous pouvons démontrer formellement en termes mathématiques reflète le même principe sous-jacent à la composition créatrice dans les formes classiques (c’est-à-dire anti-romantique, anti-moderniste) dans la poésie, le drame, la musique et la peinture. C’est le développement complet de l’esprit, comme la poésie, le drame, la musique et la peinture en caractérisent l’étendue, qui est le générateur de ce progrès car les compositions créatrices dans les formes d’art classique sont les principaux moyens par lesquels sont développées les capacités individuelles pour le travail créatif scientifique.
La fonction de la physique mathématique est correctement définie en termes formels, lorsque c’est fait comme dans la thèse de Riemann. Nous sommes sujet – et objet – de l’action d’un univers que nous ne voyons pas avec nos impressions sensorielles, un univers dont les reflets visualisables sont les ombres que l’univers réel projette sur les écrans combinés de notre imagination visuelle et auditive. Grâce aux ruses scientifiques d’une « géodésie » supérieure, la tâche de la physique mathématique est de décoder ces actions qui nous sont représentées au moyen de ces ombres sensorielles pour en tirer la réalité de cet univers réel qui existe seulement en dehors de la compétence de nos impressions purement sensorielles.
Si nous pouvons prouver de cette façon qu’il y a des changements dans les actions ombrageuses ne pouvant être expliqués par les actions des ombres, en tant qu’ombres, sur ces ombres, et qu’en fait ces actions appartiennent à un univers ayant une courbure différente de celle de notre imagination visuelle, alors nous avons montré que Platon avait raison sur ce point et que tous ses critiques étaient dans l’erreur la plus fondamentale.
Si tel est le cas, alors la notion de l’expression ontologiquement première de l’existence est rejetée loin d’Aristote et de ses imitateurs ergoteurs à « l’allure trotskiste ». Ce qui est ontologiquement premier, c’est le changement, et c’est sur lui que sont basées les mesures géodésiques de l’espace-temps physique. [29]
Si tel est le cas, alors nous ne pouvons pas extrapoler « les lois du mouvement » à partir de postulats concernant des interactions percussives ou irradiantes entre des ombres vues ou supposées. [30]
Nous devons plutôt démontrer que les lois du mouvement – ou les lois régissant des changements analogues – existent sous la forme de lois qui agissent « de l’extérieur » comme des contraintes externes sur les mouvements des ombres. Ces lois sont représentées par l’évaluation la plus élevée des principes – de la forme d’hypothèse supérieure – engendrés par les découvertes créatrices pour devenir notre niveau actuel de connaissance. Donc, à la place des hypothèses mécanistes de Galilée et de Newton sur le mouvement, nous devons substituer l’universalité de la « moindre contrainte » – contrainte par la loi dont le reflet nous apparaît comme l’hypothèse supérieure.
La première physique mathématique complète développée par Kepler à partir de l’unicité des cinq solides réguliers de Platon représente, avant Leibniz, l’un des meilleurs exemples de l’application de ce principe de « moindre contrainte ». C’est pourquoi Kepler emploie « raison » là où ses plagiaires, Galilée et Newton, utilisent le terme mécaniste de « cause ».
A partir du moment où nous avons admis l’application importante d’un tel principe de moindre contrainte, les relations entre les actions qui nous sont reflétées comme des ombres, doivent être jugées conformément à la contrainte commune que ces actions inter-agissantes doivent satisfaire. Ainsi, la notion d’une certaine courbure non nulle de l’espace-temps physique reflétée comme une ombre sur l’imagination visuelle est la plus importante conception qui marche de toute la physique mathématique.
En conclusion : la métaphore
J’ai donné de nouveaux développements plus ou moins adéquats aux autres éléments principaux de cette question dans des publications récentes (en plus de l’élaboration des mêmes sujets sous forme écrite ou lors de conférences au cours des dernières décennies). Néanmoins, le trait caractéristique suivant de la métaphore nécessite que l’on s’y attarde un instant.
Toute connaissance humaine rationnelle découle d’une définition rigoureuse de la distinction absolue entre un acte mental de découverte créatrice valide et une simple opinion déductive qui, elle, est basée sur la référence à une autorité. Sans des fondements solides ancrés dans cette condition préalable, tout ce qui est dit au nom de la philosophie en général ou de la science en particulier est une affirmation non prouvée. La notion platonicienne d’hypothèse supérieure, dont j’ai régulièrement exposé l’interprétation prouvable (régénérable), est la condition préalable à toute affirmation compétente sur ces questions de principes fondamentaux en philosophie en général ou en science en particulier. C’est là, par rapport à une notion explicite de cette hypothèse supérieure, que s’enracinent toute véritable connaissance humaine et toute notion de réalité ontologique.
Aujourd’hui, la difficulté principale dans toute la civilisation européenne (en particulier), peut être justement décrite comme étant une difficulté d’opinion fausse. Cette opinion fausse découle de la réaffirmation par Venise, à partir du XVIe siècle, de l’autorité de la méthode aristotélicienne.
La caractéristique centrale de la damnation vénitienne de l’âme humaine se retrouve chez Pomponazzi, chez Zorzi (le conseiller d’Henri VIII), chez l’influent Bellarmin et son contemporain Paolo Sarpi.
La guerre que mena Venise contre la méthode de la Docta ignorantia du cardinal Nicolas de Cues est typique de la ruse employée pour assurer cette damnation : l’argument vénitien selon lequel la base de la connaissance est l’interprétation des impressions sensorielles – ce qui exclut les idées mêmes par lesquelles on parvient aux découvertes de révolution axiomatique dans la connaissance.
Donc, sur cette base, on pourrait dire, par exemple, qu’aucun adepte de la méthode aristotélicienne ne peut être un chrétien ou un disciple juif de Moïse car ce qui sépare l’homme de la bête, ce qui place l’homme au-dessus de la bête, c’est le pouvoir de la raison créatrice, la qualité de raison créatrice qui définit l’homme comme étant à l’image du Créateur.
La raison créatrice est la substance de l’âme humaine, dont l’aristotélicien Pomponazzi niait être doué (sinon, peut-être, de façon orphique, comme récompense lors de son entrée dans l’Hadès). La raison créatrice est imago Dei et capax Dei ; sans elle, il n’y a ni imago Dei ni capax Dei.
C’est ici que repose l’objection clé que l’oligarchie vénitienne formula contre la chrétienté, lorsqu’il fallut déterminer si le pauvre possède la raison créatrice (et donc une âme). Aujourd’hui, l’oligarchie vénitienne internationale est dirigée par le « Primate parmi les Parasites » de notre temps, le « Doge d’Edimbourg » de la famille royale britannique. [31]
Pour ces oligarques, comme pour les tyrans malfaisants de la Tyre thalassocrate de Canaan, modèle de Venise et de la Compagnie britannique des Indes orientales, les classes inférieures ne doivent pas être éduquées « au-delà de leur condition », ni trop bien nourries, de crainte que ces classes inférieures ne deviennent plus nombreuses que ne le souhaitent les classes supérieures, ou bien de crainte que ces classes inférieures ne soient amenées à croire que leurs membres sont au moins autant faits à l’image de Dieu que ces membres décadents, voire « dégénérés », des familles royales et oligarchiques actuelles.
Bref, si l’idée venait à se répandre que chacun de nous est également fait à l’image du Créateur, dès sa naissance en vertu des pouvoirs créateurs qu’il possède et que les bêtes ne possèdent pas, les heures de l’usure, du malthusianisme et d’autres expressions de dégénérescence oligarchique seraient comptées. Cela, l’oligarchie ne peut le tolérer. Voilà pourquoi se perpétue le parti vénitien, dont les quartiers généraux actuels sont généralement considérés comme étant le centre financier de Londres, sa monarchie, et les laquais servant ces potentats.
Pour éclaircir cette question d’une façon très inélégante mais cependant exacte, l’augmentation du potentiel de densité de population de l’espèce humaine au-dessus de celle des grands singes est due entièrement à ce qui est justement décrit, bien que de façon imprécise, comme des améliorations dans la culture. Celles-ci sont entièrement le produit de nouvelles idées engendrées par l’aptitude que possède l’humanité à opérer des changements d’idées que la logique formelle considère comme des « révolutions axiomatiques ». L’homme, contrairement à toutes les autres espèces, est une espèce qui se reproduit par la production d’idées ; idées dont l’existence dépend de la faculté spéciale, quelque mutilée qu’elle soit, présente même chez ces oligarques qui la nient. Ainsi, l’histoire de l’humanité est l’histoire des idées, une histoire qui ne peut être jugée de façon compétente sinon par référence à cette entité – la raison créatrice, celle qui met l’existence de l’homme au-dessus de celle de la bête – dont toute méthode aristotélicienne nie implicitement l’existence.
La conscience de cette distinction est la qualité essentielle de la capacité de l’individu à atteindre un sens valide d’identité personnelle. Chaque fois qu’une personne réalise une découverte de révolution axiomatique, par exemple grâce à une hypothèse scientifique, ou une percée comparable en art ou, au moins, en re-expérimentant l’acte de découverte des découvreurs scientifiques antérieurs ou des artistes créateurs classiques, cette personne participe à une idée, un principe important dans l’histoire du monde et qui bénéfice à toute l’humanité. C’est de cette façon, et de cette façon seulement, que l’individu peut participer à l’accomplissement du travail des générations passées et contribuer à l’avancement de toute l’humanité présente et future.
Celui ou celle qui atteint un sens conscient de sa participation à l’histoire par ses propres pouvoirs de raison créatrice, cesse d’être un individu dans l’ici et le maintenant immédiat d’un troupeau humain, et devient consciemment un participant à l’ensemble de l’humanité. Cette personne n’est pas un esclave, ni un serf. Elle est qualifiée pour voter intelligemment, pour parler dans les assemblées d’une démocratie républicaine ou pour remplir d’autres fonctions exécutives dans la société. Dans une société prudente, ce serait la qualification minimale requise comme condition préalable pour qu’un individu puisse remplir l’une de ces fonctions.
Sans de telles qualifications, l’individu est un pauvre hère tragique, soit un Don Quichotte vivant astucieusement dans un monde de fantaisie, soit un Sancho Pança ne pouvant jamais réussir à gouverner une île parce que sa tête ne peut gouverner les passions situées en dessous de la ceinture.
Pour de telles raisons, depuis que Paolo Sarpi et sa faction convinrent qu’il était préférable de prendre le contrôle et de corrompre les nouvelles institutions de la science plutôt que de chercher à les supprimer par la force brutale, leur principale préoccupation a été d’amener l’espèce humaine à un abêtissement général, en excluant des mathématiques et d’autres modes de représentations scientifiques toute considération du principe créateur de découverte.
Sarpi joua un rôle direct en mettant au point cette pratique grâce aux bons services de Galilée, Robert Fludd et Francis Bacon. Descartes et Newton caractérisent dans l’histoire des institutions scientifiques véritables ou prétendument telles, la longue liste d’individus intellectuellement destructeurs contrôlés par Venise.
Au XVIIIe siècle, Voltaire, Maupertuis, Algarotti, Euler, Lagrange et Lambert de l’Académie de Berlin ainsi que les encyclopédistes français sont représentatifs de ces individus influents corrompus qui, sous le contrôle d’agents de renseignement vénitiens comme Conti et Algarotti, opéraient à l’intérieur des institutions scientifiques pour éliminer la tradition scientifique héritée du Cusain, de Léonard de Vinci, de Kepler et de Leibniz. Emmanuel Kant, le marquis de Laplace, Augustin Cauchy ainsi que certains cercles allemands et d’autres sous le contrôle de lord Kelvin, sont représentatifs de la continuation de la tradition vénitienne durant le XIXe siècle.
Ainsi, du fait de l’influence du culte empiriste de Paolo Sarpi, et d’autres influences semblables, on trouve la marque la plus populaire de la pratique pseudo scientifique dans la méthode développée par l’éternellement puéril savant idiot John Von Neumann, dans son livre écrit avec Oskar Morgenstern, La théorie des jeux et du comportement économique, dans lequel les auteurs basent entièrement leur dogme sur les axiomes du « modèle Robinson Crusoé ». [32]
De la même manière, l’étudiant scientifique naïf ou mal éduqué imagine que son observation de la « reproductibilité » d’un phénomène fait partie intrinsèque de la nature de la preuve scientifique, ou encore que la science est statistique. Ne pas se considérer soi-même comme étant imago Dei et capax Dei, en termes de conscience de génération d’hypothèses au moyen d’actes mentaux créateurs, amène à tolérer la condition de servage universitaire et provoque le malheur de l’homme qui aurait pu devenir un scientifique s’il avait rempli la première condition préalable, c’est-à-dire se connaître soi-même comme étant fait à l’image vivante du Créateur.
Le « modèle Robinson Crusoé » reflète directement l’influence de la version de l’empirisme aristotélicien de l’école de Sarpi et les dogmes de Francis Bacon, Galilée, Thomas Hobbes, René Descartes, John Locke, Isaac Newton, David Hume, Adam Smith et al.
Ce modèle part de l’idée que l’homme est comme une bête individuelle, un individu solitaire gouverné par un répertoire intérieur de ce qu’Adam Smith décrit en ces termes :
La Nature nous a dirigé vers la plus grande part de ceux-là par des instincts immédiats et originels. La faim, la soif, la passion qui unit les deux sexes, l’amour du plaisir et la crainte de la douleur nous amènent à appliquer ces moyens pour leurs propres buts et sans aucune considération de leur tendance aux fins bienfaisantes que le grand Directeur de la nature avait l’intention de leur faire produire. [33]
Ce même argument, copié directement d’agents vénitiens comme Maupertuis et Giammaria Ortes, et proposé par Adam Smith dans La théorie des sentiments moraux (1759), a servi comme base au dogme de la « main invisible » dans ce fameux livre antiaméricain qu’est La richesse des nations (1776). [34]
Dans la réalité historique, l’existence humaine est le résultat de la génération (et de la régénération) de nouveaux théorèmes, de nouvelles hypothèses et de nouvelles hypothèses supérieures valides ; on ne peut aboutir à ce résultat que grâce au développement et à l’exercice des pouvoirs créateurs d’esprits individuels, dont l’existence est rejetée par les aristotéliciens, tels Pomponazzi et les empiristes, tandis qu’elle est déclarée inconnaissable de ce côté de l’Hadès par l’aristotélicien agnostique Emmanuel Kant des Critiques et par l’orphique Gasparo Contarini. Par conséquent, l’intérêt vital de l’espèce humaine, c’est le rôle social des pouvoirs mentaux créateurs de l’individu lorsqu’il produit et reproduit des idées dont dépend absolument l’existence continue de la société dans son ensemble. Donc, le seul individu moral est celui dont l’intérêt personnel n’est pas ce qu’Adam Smith définit comme les « instincts immédiats et originels », mais plutôt une préoccupation envers ce genre d’idées formulées et employées précisément en « considération de leur tendance pour ces fins bienfaisantes », idées clairement identifiées dans la Genèse (1 :26-28).
Toute la méthode empiriste et des Lumières des XVIIe et XVIIIe siècles est fondée sur le principe irrationnel aristotélicien qu’Adam Smith présente sous sa version radicalement gnostique. [35]
La méthode empiriste se résume toujours à deux présupposés. D’abord, le présupposé hobbesien et lockéen décrit par Smith, selon lequel l’homme est un observateur et un acteur individuel gouverné par ses instincts primaires constituant la « forme cellulaire » de toute réalité connaissable. C’est ainsi que l’on en arrive à voir Robinson Crusoé comme le fondateur aborigène de l’économie politique et de la « théorie du chaos ». Ensuite, les dogmes de la méthode déductive irrationaliste d’Aristote : la négation de l’existence de « l’étincelle divine de raison » dans la personne individuelle, la répudiation de la qualité de raison créatrice qui est caractérisée par le renversement axiomatico révolutionnaire de chaque affirmation faite par Aristote concernant soit l’existence, soit l’interprétation de phénomènes et de dogmes.
Depuis plus de deux mille ans, Aristote, par l’utilisation de cette méthode corruptrice, a été l’adversaire le plus influent de la raison et de la science et aussi la cause la plus importante de l’affaiblissement de la chrétienté. N’eussent été des influences destructrices de l’empiriste Paolo Sarpi et de ses semblables, la corruption de la science par les méthodes vénitiennes de Sarpi, caractéristique chez Galilée et Newton, aurait été évidente pour peu même qu’elle soit jamais venue à exister au sein des institutions dirigeantes de la science.
La « science politique » est exemplaire de la façon dont ce problème est aujourd’hui institutionnalisé dans notre civilisation : elle n’est qu’une pseudo science inventée par la « Madame Blavatsky » des Lumières françaises et allemandes, la fameuse Madame de Staël. [36]
Arrachons ces mensonges abominables de nos universités pour les faire plutôt résider avec l’astrologie, la sorcellerie, le malthusianisme et la phrénologie, parmi les superstitions pathétiques qui séparent les pauvres misérables ignorants des hommes et des femmes sains d’esprit.
Dans la place vacante ainsi créée dans les collèges, mettons l’étude des subterfuges vénitiens au programme de l’histoire des sciences.
S’il n’y avait eu des politiques aussi perverses aux plus hauts échelons d’autorité politique dans les institutions de la science (sans compter les oligarques charitables qui les financent et contrôlent ainsi les programmes des comités de lecture et les programmes éducatifs), la notion mécaniste de causalité n’aurait jamais supplanté le principe de raison sur lequel des individus comme Platon, Nicolas de Cues, Léonard de Vinci, Kepler et Leibniz l’avaient fondée.