Pour Kepler, la créativité est la clé pour comprendre le système solaire

[sommaire]

Megan Beets : Pour découvrir le fonctionnement du Système solaire, Johannes Kepler a utilisé ce que philosophe et théologien Nicolas de Cues (1401-1464) avait compris conceptuellement. Il a ainsi découvert scientifiquement une conception nouvelle de la relation entre l’être humain et le Système solaire.

Benjamin Deniston : Toutes les découvertes révolutionnaires de Kepler sont inscrites dans cette démarche. C’est dans cette méthode qu’il puisait ses racines et c’est cette qualité de pensée qui lui permit ensuite de faire les percées que d’autres n’ont pu faire et n’ont pas fait.

Dans un certain sens, Kepler a vraiment démontré et validé la conception philosophique de Cues sur la façon dont l’univers s’est organisé et sa relation à l’humanité.

Je voudrais énoncer quelques hypothèses en développement, en étudiant rétrospectivement certains travaux de Kepler sur l’organisation du Système solaire et en me concentrant sur sa thèse essentielle : que ni les nombres ni les mathématiques ne sont une science et que notre compréhension de l’univers repose sur notre compréhension de l’esprit humain, décrit par Cues comme un « microcosme du macrocosme ».

L’esprit humain a un potentiel unique que nous ne pouvons pas définir ni mesurer avec des paramètres traditionnels. Nous ne pouvons pas le définir par la perception des sens, par la chimie, la biologie ou autre. Nous devons étudier ce qu’est l’esprit humain lui-même et quelle est sa fonction dans la société humaine. Cela nous en dira plus sur la relation de l’humanité avec l’univers que ce que peuvent nous en apprendre les perceptions des sens.

Kepler : pas seulement une question de chiffres

La Fig. 1a provient d’un ouvrage de jeunesse de Kepler, le Mysterium Cosmographicum (1596). Il s’est demandé pourquoi les planètes sont éloignées les unes des autres de ces distances-là plutôt que d’autres.

A l’époque, on ne connaissait que six planètes du système solaire, séparées les unes des autres par cinq distances. Pourquoi ces distances ont-elles ces valeurs ?

Kepler va commencer par jouer avec cela, précisément pour écarter l’approche mathématique : « Pourrions-nous avoir seulement un ratio numérique ? Ce rapport pourrait-il être une simple proportion ? Une planète pourrait-elle être à la deuxième ce que la deuxième est à la troisième ? »

Et il montre que ce n’est pas possible, que ça ne fonctionne pas, ce qui est intéressant parce que la loi de Titius-Bode a été développée plus tard pour tenter de l’expliquer de cette manière.

Dès le départ, Kepler démontre qu’on ne peut pas se contenter d’utiliser les rapports numériques et qu’il faut utiliser les cinq solides platoniciens, qui sont des formes régulières dans l’espace tridimensionnel, pour estimer la distance entre les planètes.

Telles sont les conceptions en jeu dans le Mysterium Cosmographicum. Ensuite, dans son ouvrage La Nouvelle Astronomie (1609), Kepler opère une autre révolution, en découvrant que les planètes n’ont pas une orbite circulaire : la distance entre les planètes et le Soleil change constamment.

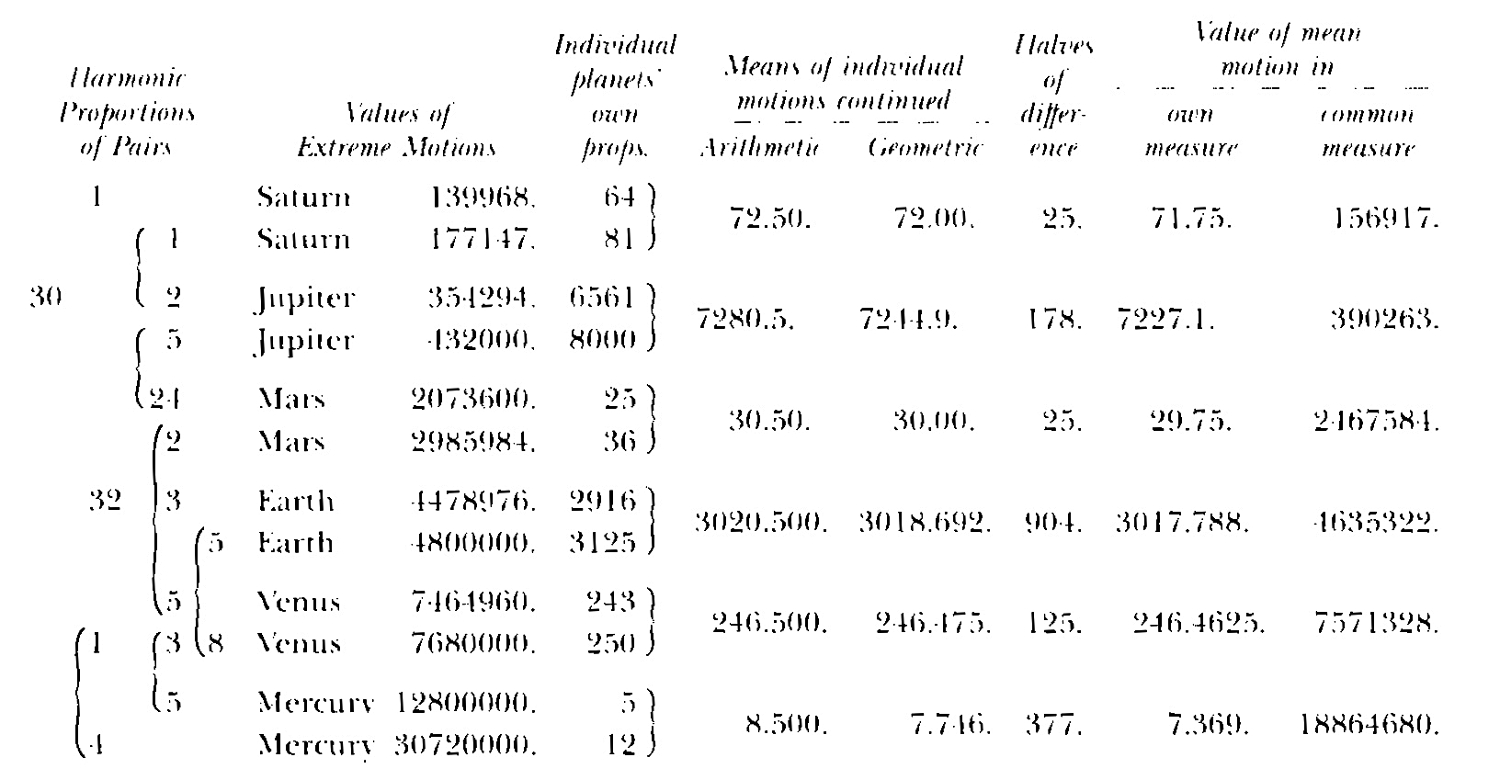
Cependant, il va plus loin. Dans L’Harmonie du Monde (1619), il explique qu’il n’y a pas seulement une distance entre chaque planète et le Soleil, mais une « série » de distances : vous avez la distance la plus éloignée du Soleil, dite aphélie, et la distance la plus proche, ou périhélie (Fig. 1b).

La plus haute orbite est celle de Saturne. Vous pouvez voir trois cercles, représentant trois distances entre Saturne et le Soleil : la plus éloignée, la plus proche et la moyenne entre les deux.

Vers la fin de sa vie, Kepler se demande à nouveau pourquoi on a ces distances et pas d’autres. Ces différences sont attribuées à l’excentricité de l’orbite.

Il se repose alors la question : pourquoi les planètes ont-elles ces distances et ces excentricités particulières ?

Il arrive à la conclusion qu’on doit aborder cela d’un point de vue musical : on doit examiner les intervalles créés par les mouvements extrêmes des planètes, comparer les mouvements extrêmes d’une seule planète et ceux des différentes planètes entre elles.

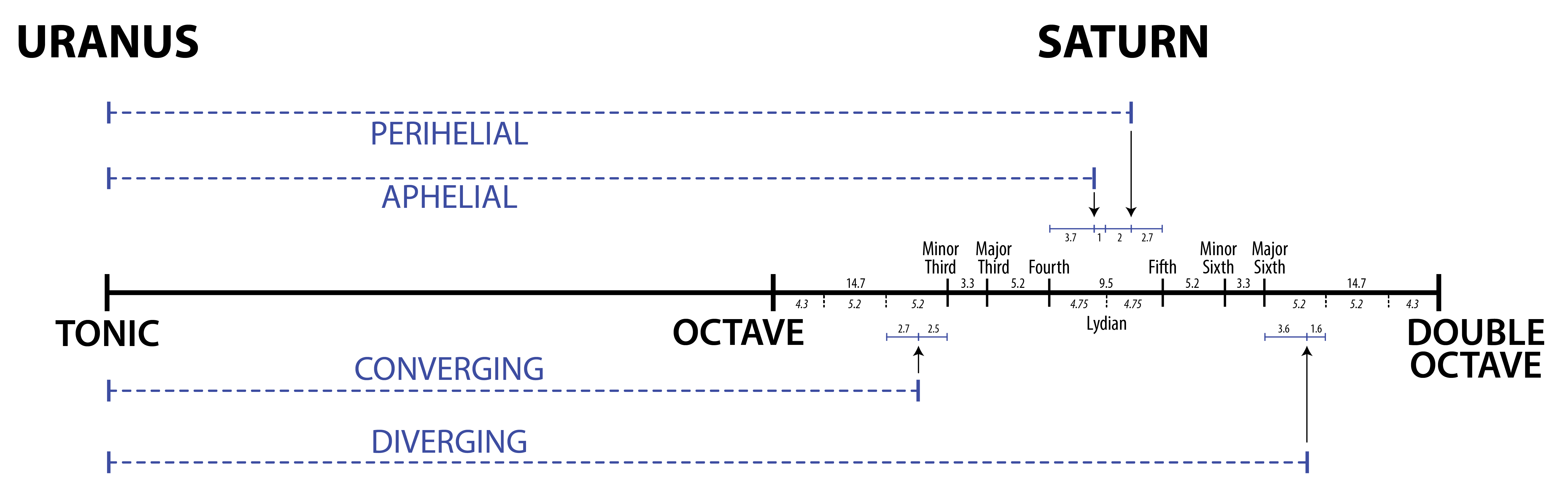
La Fig. 2 montre deux planètes, une planète « intérieure » et une planète « extérieure ». Vous pouvez voir que si leurs orbites étaient circulaires, elles correspondraient à la ligne bleue en pointillé, mais leurs orbites sont elliptiques, avec un certain degré d’excentricité dans leur distance par rapport au Soleil.

Ce que Kepler observe, ce sont les différentes relations entre les mouvements de ces planètes à leurs extrêmes.

Ainsi, par exemple, la planète intérieure, la rouge, est assez proche de sa distance la plus éloignée du Soleil, où elle se déplacerait le plus lentement. Et la planète extérieure, la verte, est quasiment à sa distance la plus proche du Soleil, où elle se déplacerait le plus vite.

Les harmonies musicales

Je vais donner un aperçu de plus de 600 pages de travaux (qui devraient évidemment être travaillées en détail) et les utiliser comme base pour des découvertes plus récentes.

Kepler est guidé par l’idée qu’il faut regarder les mouvements apparents à ces extrêmes et rechercher les caractéristiques que nous associons aux harmonies musicales. Et pour chaque orbite, il compare les mouvements « extrêmes », le plus rapide et le plus lent, définissant ainsi un certain intervalle, ce qui permet la recherche des intervalles harmoniques qui peuvent être mesurés. Ensuite, il observe les planètes voisines, la planète « intérieure » et la planète « extérieure ».

Il met ainsi en lumière quatre types de relations, qui sont comme des conditions « limites ». Chaque planète a un point de son orbite où sa vitesse est la plus rapide et un point où elle est la plus lente ; vous pouvez comparer pour chacune le point le plus rapide et le plus lent, puis comparer entre eux les points les plus rapides avec les plus lents. Kepler les appellent mouvements convergents lorsque leurs vitesses sont les plus proches les unes des autres, et mouvements divergents lorsque l’on a la plus grande différence entre les vitesses ; les mouvements à l’aphélie, lorsqu’ils sont à leurs distances respectives les plus éloignées, et au périhélie lorsqu’ils sont à leurs distances respectives les plus proches.

La question est toujours la même : pourquoi le système solaire est-il organisé de cette façon et pas autrement ? Nous avons une certaine conception de l’éloignement entre les planètes grâce à l’utilisation des cinq solides platoniciens, mais nous savons également que ces planètes ont des excentricités particulières.

Pourquoi celles-ci et pas d’autres ? En examinant les relations entre les mouvements extrêmes, Kepler met à jour toute une organisation harmonique du Système solaire : un système harmonique musical est nécessaire pour comprendre pourquoi les excentricités sont ce qu’elles sont. Ça lui permet de revenir en arrière après avoir utilisé ces rapports harmoniques exposés plus loin (Tableau 1) pour définir le Système solaire et recalculer plus précisément, grâce aux harmoniques, les distances et les excentricités. Enfin, il commence par ce qu’il définit comme les intervalles harmoniques nécessaires pour n’importe quelle planète individuelle et certaines paires de planètes. De là, il définit le Système solaire comme le produit de cette organisation harmonique nécessaire.

Beets : Par « nécessaire », je pense que cela rappelle beaucoup ce que fait Nicolas de Cues dans sa Docte ignorance. Cues ne fonde pas sa pensée sur de quelconques données ou observations, mais sur ce qui devrait exister, en s’appuyant sur des principes fondamentaux. C’est aussi ce qu’a fait Kepler. Guidé par les données et sa connaissance des mouvements planétaires, il remonte lui aussi aux causes premières : quels doivent être les mouvements pour que le système soit le plus harmonique possible ? Puis il en tire quelle devrait être la distance.

Deniston : Exactement. Le seul exemple qui me vienne à l’esprit est l’observation qu’il fait des mouvements de la Terre et de Vénus. En effet, Kepler dit que le Système solaire devrait contenir la distinction entre mode majeur et mode mineur ou, comme il le dit, entre mode dur et mode mou. Cette distinction faisant partie du système musical, elle doit donc également exister dans le Système solaire, si l’on se réfère aux causes premières.

Le Système solaire doit être le reflet de notre conception de l’harmonie musicale, et c’est ce que nous voyons dans la relation entre la Terre et Vénus. Il ne part donc pas seulement des données, mais de ce qui devrait être nécessaire si l’univers est organisé par cette conception harmonique que seule l’humanité peut définir et comprendre. Je pense qu’il est opportun d’introduire ce tableau (Tableau 1). Kepler annonce qu’il va se lancer dans un calcul qui n’a jamais été effectué avant dans l’histoire humaine – à savoir, dériver les distances et les excentricités des planètes de l’organisation harmonique du Système solaire.

Il y a beaucoup à dire à propos de ce travail. Toute la vie de Kepler est déterminée par ce travail révolutionnaire qui démontre la validité des conceptions de Nicolas de Cues : le fondement de la science part de la compréhension de l’esprit humain comme expression de l’organisation de l’univers.

Il y a quelques années, en faisant des recherches, j’ai été confronté à quelque chose de provocant : suite à la révolution scientifique de Kepler, une série de nouvelles planètes ont été découvertes, en particulier Uranus et Neptune. Nous avons la ceinture d’astéroïdes, que nous allons garder pour une autre fois. Mais nous avons aussi ces deux planètes découvertes après l’époque de Kepler. Les seules planètes alors connues étaient Mercure, Vénus, la Terre, Mars, Jupiter et Saturne.

Si vous vous demandez quand nous avons découvert ces planètes, vous n’aurez pas de réponse. Aussi loin que l’on remonte, ces planètes étaient connues. Kepler avait accès à une certaine compréhension du Système solaire du fait de la connaissance de ces objets observables directement dans le ciel, les six planètes du système.

Ce n’est que suite aux découvertes de Kepler, et avec le développement des télescopes ainsi que l’application des découvertes de Kepler – ses lois sur le mouvement des planètes – que nous avons pu découvrir et identifier ces deux planètes supplémentaires. Uranus a été découverte dans les années 1780 par William Herschel, grâce à un télescope de sept pieds de long qu’il avait construit lui-même (la Fig. 3 est une réplique).

C’était indispensable, car Uranus ne peut pas être vue facilement et il faut développer un système télescopique assez sophistiqué pour l’apercevoir.

Jason Ross : C’est impossible de le voir sans télescope, non ?

Deniston : A moins de savoir exactement où elle se trouve, avec un ciel parfaitement dégagé et une très bonne visibilité, on pourrait peut-être apercevoir quelque chose qui ressemble à une étoile de luminosité très faible. Je pense que c’est la raison pour laquelle nous n’avons connu que les six autres pendant si longtemps. C’est seulement grâce au développement des systèmes télescopiques que nous avons pu identifier Uranus comme étant une planète. Neptune a été découverte un peu moins d’un siècle plus tard, et d’une façon assez intéressante.

Certains chercheurs ayant remarqué une différence dans le mouvement d’Uranus par rapport à ce à quoi ils s’attendaient, ils ont fait l’hypothèse qu’un autre corps planétaire agissait peut-être sur lui. C’est un travail très intéressant qui a pu aboutir grâce aux découvertes de Kepler, notamment sur le télescope. Kepler a beaucoup travaillé sur l’optique et a découvert des principes intéressants sur ce type de perception sensorielle.

La découverte de Neptune elle-même nécessite de comprendre les lois qui régissent Uranus. A la suite et en conséquence des travaux de Kepler, nous avons découvert deux planètes supplémentaires. La question à laquelle je voudrais répondre est : comment s’intègrent-elles dans le système harmonique de Kepler ? Je vais avancer quelques hypothèses, et bien que cela nécessite plus de travail pour arriver à une conclusion, les éléments que je vais vous montrer sont assez provocants et pointent dans la bonne direction.

L’anomalie d’Uranus et de Neptune

Nous allons donc examiner les mouvements d’Uranus et de Neptune du point de vue de la méthode utilisée par Kepler, en comparant leurs mouvements aux extrêmes (Tableau 2).

Si vous prenez le mouvement apparent d’Uranus à son point le plus proche du Soleil, quand il est le plus rapide, et que vous le comparez à son mouvement apparent le plus éloigné du Soleil, où il est le plus lent, et que vous calculez la proportion entre les deux, qu’obtenez-vous ? Vous prenez simplement les données dont dispose la NASA et vous obtenez un intervalle de 0,83308 etc. Cet intervalle est très proche de l’intervalle musical de la tierce mineure.

Or, si vous regardez effectivement l’harmonie la plus proche de cet intervalle sous forme décimale, vous pouvez voir combien il y a de « commas » (intervalle musical beaucoup plus petit que la différence entre deux touches voisines sur un piano) entre celui-ci et l’harmonie la plus proche : il n’y a presque rien, précisément une tierce mineure.

Beets : Juste pour clarifier les choses – parce que beaucoup de gens ne sont pas habitués à penser les mouvements des planètes en termes d’intervalles – prenez deux cordes d’un violoncelle, par exemple. Lorsque les cordes vibrent, les notes graves sont générées par une vibration lente et les aiguës par une vibration plus rapide. Et si vous accordez ces cordes de telle manière que le rapport entre elles soit le même qu’entre les deux mouvements extrêmes d’Uranus, le son que vous entendrez sera presque identique à une harmonie musicale, à des notes de la gamme musicale.

Deniston : Exactement. Nous pouvons faire la même chose pour Neptune et nous obtenons quelque chose de très proche de ce que Kepler appelle un intervalle mélodique, 24/25, un demi-ton. Il s’agit de la différence entre une tierce majeure et une tierce mineure, ou entre une sixte majeure et une sixte mineure. En étudiant les mouvements propres à chaque planète, nous obtenons des valeurs très intéressantes.

Nous pouvons passer à l’étape suivante et nous demander quelle est la relation entre Uranus et Neptune. Ces deux planètes qui nous étaient inconnues jusqu’à récemment, nous allons comparer leurs intervalles. Là encore, il y en a quatre : le convergent, le divergent, l’intervalle à l’aphélie et celui au périhélie. L’intervalle où Uranus est le plus éloigné à celui où Neptune est le plus éloigné (du Soleil), celui où elles sont le plus proche.

Et enfin les mouvements divergents, du plus éloigné d’Uranus au plus proche de Neptune, et du plus proche de Neptune au plus éloigné d’Uranus. On crée ainsi quatre combinaisons. En étudiant les intervalles entre Uranus et Neptune, nous pouvons regarder comment elles « chantent » entre elles, et quels sont les intervalles de leurs mouvements extrêmes.

Vous obtenez ainsi une série de valeurs assez intéressantes, toute une série d’intervalles mélodiques, qui ne sont pas harmoniques au sens habituel. Si vous jouiez l’un de ces intervalles sur un piano, le son obtenu ne serait pas très beau. Mais ces intervalles sont nécessaires au système musical. Ce sont les demi-tons ou les intervalles de septième (intervalle dissonant).

Vous pouvez le voir ici (Tableau 3) : nous avons les mouvements convergents entre le mouvement le plus lent de Neptune et le mouvement le plus rapide d’Uranus, qui génère un intervalle de septième. Pour les mouvements divergents — entre le mouvement le plus lent d’Uranus et le mouvement le plus rapide de Neptune — nous obtenons une octave augmentée d’un ton mineur. Les mouvements à l’aphélie créent un autre intervalle de septième, et les mouvements au périhélie créent une octave augmentée d’un dièse. Tous les mouvements existant entre Uranus et Neptune créent des intervalles mélodiques.

Beets : Ils ont une position dans la gamme musicale, mais si vous les écoutez, vous vous rendrez compte qu’ils sont dissonants. Ils ne sont pas arbitraires et existent dans la gamme musicale, mais ils ne sont pas beaux ni harmoniques, contrairement aux intervalles des autres planètes.

Deniston : Pris en eux-mêmes, c’est vrai. Mais il faut repenser à l’ensemble du travail de Kepler. Il a défini les intervalles mélodiques comme une partie nécessaire du système harmonique, commençant par les intervalles harmoniques pour continuer avec les intervalles mélodiques, ce qui permet de définir toute la gamme musicale. Les intervalles mélodiques sont par ailleurs dérivés des intervalles harmoniques. Après Uranus et Neptune, nous pouvons regarder ce qui se passe entre Saturne et Uranus. Saturne est une planète que Kepler connaissait déjà, et Uranus est la première nouvelle planète que nous ayons découverte. Il s’agit donc de la frontière entre celles que nous avons découvertes et celles connues depuis l’Antiquité. Quel type d’intervalles avons-nous là ? Nous obtenons une série d’intervalles plutôt dissonants (Tableau 4).

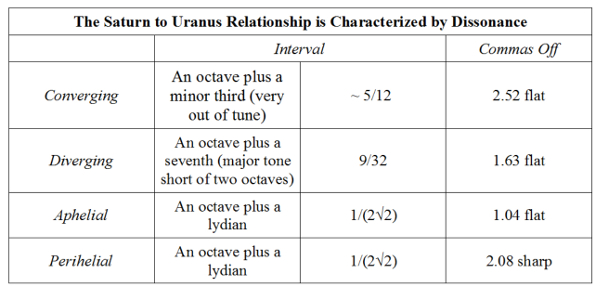
Le mouvement convergent s’approche d’une octave augmentée d’une tierce mineure (nous y reviendrons plus tard). Il y a un écart de deux commas et demi (ce qui est « énorme ») entre les mouvements convergents et cette proportion. Le mouvement divergent — l’intervalle le plus extrême entre deux planètes — n’est pas tout à fait une octave augmentée d’une septième, donc pas tout à fait une octave et un intervalle mélodique.

Les intervalles à l’aphélie et au périhélie sont très proches d’un intervalle très dissonant appelé le lydien, qui se situe entre la quarte et la quinte, un intervalle dissonant unique qui joue un rôle très important dans l’ensemble du système musical, mais qui est en lui-même très discordant.

Les intervalles générés entre Uranus et Neptune étaient tous des intervalles mélodiques, mais les intervalles entre Uranus et Saturne ressemblent à une série de dissonances. Il y a encore un troisième phénomène à étudier, mais avant cela, on peut se poser une question intéressante : pourquoi ces intervalles ont-ils ces caractéristiques si particulières et quelle est la relation entre Uranus et Neptune d’une part et le reste des planètes, ainsi que l’ensemble du système.

Quand j’ai observé cela pour la première fois il y a quelques années, j’ai pensé : Uranus et Neptune vont remplir le rôle de nouvelles notes dans le système et permettre de fournir des possibilités nouvelles qui n’existaient pas avec les notes fournies par les seules planètes que Kepler connaissait.

En y regardant de plus près, je me suis aperçu que ce n’était pas le cas, qu’elles utilisaient les mêmes notes que toutes les autres planètes, mais éloignées d’un certain nombre d’octaves.

Si vous prenez Uranus et que son périhélie « chante » la note C (do dans la notation musicale), Vénus, à son périhélie, « chantera » aussi la note C, mais sept octaves plus haut. De fait, il y a plusieurs octaves de différence entre les mouvements extrêmes d’Uranus et de Neptune et ceux des autres planètes.

Vous pouvez voir la comparaison au Tableau 5 : Uranus avec Vénus, l’aphélie d’Uranus avec celui de Mercure, et l’aphélie de Neptune avec le périhélie de Jupiter. Il s’agit de la même note, mais à une autre octave dans le système musical. Nous avons mis au jour des caractéristiques très distinctes dans chacun de ces travaux : si vous étudiez la relation entre Saturne et Uranus, à la frontière entre les planètes que nous connaissons depuis des siècles et les nouvelles, vous vous apercevez que tous les intervalles sont dissonants. Si vous étudiez la relation entre Uranus et Neptune, les deux nouvelles planètes ensemble, vous vous apercevez que tous les intervalles sont mélodiques.

Et si vous étudiez la relation des deux nouvelles planètes avec l’ensemble du système, vous vous apercevez que les intervalles entre les mouvements extrêmes sont définis par les octaves. Tout cela est fascinant, parce que lorsqu’on examine la relation de Neptune et Uranus avec toutes les autres planètes, on n’obtient pas quelques intervalles dissonants, quelques intervalles mélodiques et quelques octaves, tous les intervalles mis en évidence sont des octaves.

Lorsque l’on étudie la relation particulière entre Saturne et Uranus, on n’obtient pas des intervalles mélodiques ou des octaves, mais uniquement des intervalles dissonants. Et lorsque vous étudiez la relation entre Uranus et Neptune, vous n’obtenez pas un intervalle lydien, quelques octaves et des intervalles mélodiques, vous n’obtenez que des intervalles mélodiques. Chacun de ces rapports montre qu’une caractéristique très particulière s’y exprime clairement. Vous vous apercevez que ces deux nouvelles planètes se conduisent de trois façons différentes entre elles et par rapport au reste du système.

D’où provient la dissonance ?

Si l’on part de la conception du Cusain sur la relation entre l’homme et l’univers, comme Kepler le développe avec sa propre conception harmonique du Système solaire, pourquoi est-il nécessaire que ces deux nouvelles planètes engendrent ces trois caractéristiques particulières ?

Premièrement, regardons de plus près la relation entre Uranus et Saturne, celle qui crée tous ces intervalles dissonants (Fig. 4). Si nous prenons les mesures que nous avons déjà prises avec Uranus, nous pouvons voir que tous les intervalles sont supérieurs à une octave, mais que l’intervalle des mouvements convergents n’atteint pas tout à fait une octave augmentée d’une tierce mineure, il est supérieur à l’octave de sorte qu’il atterrit dans cette tranche dissonante. L’intervalle des mouvements divergents se rapproche un peu plus d’une octave augmentée d’une septième, mais il n’atteint pas tout à fait la septième, tout en étant au-dessus d’une octave augmentée d’une sixte majeure, de sorte qu’il n’atteint pas cet intervalle harmonique.

Et il y a encore plus intéressant, avec les intervalles à l’aphélie et au périhélie qui convergent étroitement de part et d’autre du lydien, cet intervalle extrêmement dissonant. Il n’y a que cette paire de planètes, et aucune autre, qui présente ce type de structure dissonante. Aucune des planètes que Kepler a examinées n’a cette caractéristique. Il y a ici un problème nécessaire au maintien de l’ensemble du système en harmonie.

Ross : Le couple Uranus-Neptune n’est pas dissonant, comme tu l’as montré auparavant.

Deniston : Non, il se caractérise par une très grande proximité avec les intervalles mélodiques. Pourquoi y a-t-il donc cette « qualité » dissonante entre Uranus et Saturne ? (Fig. 4)

Eh bien, je pense qu’il existe aussi une dissonance dans la relation entre l’humanité et le Système solaire, et que nous avons en fait à étudier deux systèmes : les six premières planètes étant connues depuis des milliers d’années, il y a eu un bond qualitatif dans la relation entre l’humanité et le Système solaire, que l’on peut associer à la frontière entre les six planètes connues des anciens et la découverte de ces deux planètes à l’ère moderne.

Cela exprime un changement, non seulement dans le nombre de planètes que l’humanité connaît, mais aussi dans l’humanité elle-même. Il s’agit de la qualité de relation entre l’humanité et le Système solaire créée par Cues et Kepler, une étape qualitativement supérieure des capacités mentales de l’humanité dans sa relation avec l’univers.

C’est en ce sens qu’il y a dissonance, ce qui s’exprime directement dans la dissonance des intervalles eux-mêmes à l’intérieur du Système solaire. Si l’on revient à la relation Uranus-Neptune, nous avons cette dissonance qui sépare les deux nouvelles planètes de celles qui étaient déjà connues auparavant, une dissonance dans les intervalles musicaux eux-mêmes et également dans la relation entre l’humanité et le Système solaire.

Quant à la relation entre les deux planètes elles-mêmes, elle est définie par tous ces intervalles mélodiques, qui ne sont pas véritablement accessibles aux sens eux-mêmes. En jouant sur un monocorde, vous pourriez définir et trouver les intervalles harmoniques, en créant des sons qui sonnent bien. Vous pourriez les identifier de cette manière, ce qui n’est pas possible avec les intervalles mélodiques. Vous pourriez peut-être les identifier en sachant déjà à quoi ils ressemblent, mais sans une connaissance a priori, c’est impossible.

Beets : La résonance des intervalles harmoniques est naturelle. Deux cordes accordées en fonction d’un intervalle harmonique résonnent physiquement ensemble. Mais deux cordes accordées en fonction d’un intervalle mélodique seront dissonantes et ne vont pas résonner ensemble.

L’esprit humain et le système solaire

Deniston : En développant un système musical basé sur le système des intervalles harmoniques, comme le fait Kepler dans le livre trois de L’Harmonie du monde, et en faisant appel à la raison humaine, comment créer un système dont les intervalles mélodiques soient la caractéristique nécessaire ? Les définir nécessite d’aller au-delà des capacités sensorielles et de faire appel à la raison pour délimiter les frontières du véritable système.

Si vous voulez discuter de la caractéristique générale des intervalles mélodiques, vous découvrirez qu’ils sont le produit du travail de l’humanité avec les intervalles harmoniques et qu’ils définissent un système, ce qui vous permet de les identifier comme quelque chose d’existant et d’important, comme une partie du système, mais qui n’est pas directement accessible aux perceptions des sens.

Voilà donc ce qu’est la qualité de la relation entre Uranus et Neptune, et il s’agit également de la qualité de notre relation avec ces planètes. Je pense que la solution ne peut être trouvée qu’en partant de la relation entre l’esprit humain et le Système solaire. Uranus et Neptune étant inaccessibles aux seules perceptions sensorielles, l’humanité a dû développer des instruments artificiels, des appareils télescopiques.

De plus, dans le cas de Neptune, il a fallu la compréhension des mouvements planétaires de Kepler et du fonctionnement de tout le système planétaire pour pouvoir l’identifier. Dans un certain sens, la qualité de la relation de l’humanité avec Uranus et Neptune est la même que celle de la relation entre les intervalles mélodiques et harmoniques. En allant au-delà de cette condition-limite, on résout cette dissonance, tout en ayant accès à une qualité qui transcende les perceptions sensorielles.

En dépassant cette dissonance, dans le sens de la relation de l’humanité avec ces planètes extérieures, nous allons au-delà de la perception sensorielle directe, dans un domaine où notre système de perception est subsumé par des principes plus élevés.

L’étude de ces deux planètes met en lumière une troisième qualité unique : lorsque nous comparions Uranus et Neptune, et leurs mouvements avec ceux des autres planètes du Système solaire, on obtenait toute une série de relations définies par les octaves (Fig. 5).

Cela définit une délimitation très intéressante du Système solaire dans son ensemble : les deux planètes les plus éloignées du soleil engendrent une série d’octaves délimitant le système avec les deux planètes les plus proches du Soleil. Neptune s’harmonise directement avec le périhélie de Mercure et l’aphélie de Vénus.

Dans le même temps, l’aphélie de Neptune s’harmonise avec le périhélie de Jupiter. Et Vénus s’harmonise autant avec Neptune qu’avec Uranus. Ainsi, dans l’ensemble, nous avons la caractéristique dissonante entre Uranus et Saturne, la caractéristique mélodique entre Uranus et Neptune, et enfin, la relation Uranus et Neptune d’un côté et les autres planètes de l’autre, délimitant l’ensemble du système par des octaves. Nous avons affaire à un phénomène très provocant.

Ces deux nouvelles planètes jouent un rôle très important dans le système de Kepler, mais ne peuvent être comprises que dans ce système lui-même. Ce que l’on découvre avec Cues et Kepler, c’est que la science est la compréhension de la puissance créatrice de l’esprit humain comme reflet de l’univers. La conception que Cues et Kepler élaborent, dans ce travail qui est au centre de leur vie, est celle que l’esprit humain est un reflet de l’intention créative inhérente à l’univers.

Pour paraphraser Kepler, c’est comme si le Créateur avait créé le système solaire en prévision de l’apparition de l’être humain qui y vivrait. Les qualités d’Uranus et de Neptune sont totalement cohérentes avec cette conception, nous montrant une délimitation dans la relation de l’humanité avec le Système solaire. On ne peut pas séparer le Système solaire de sa relation avec l’humanité...

Ross : Sans vouloir exagérer les connections, l’intervalle du périhélie de Mercure avec l’aphélie de Saturne est de sept octaves et demi, c’est-à-dire l’étendue exacte du clavier d’un piano. L’étendue totale de ce que tu as montré, allant du périhélie de Mercure à celui de Neptune, est de dix octaves, soit à peu près l’étendue de l’audition humaine. C’est une idée intéressante, qui peut délimiter ce dont le corps humain est capable.

Moralité et Science

Ross : Je voudrais revenir à Aristote. Beaucoup de gens nous demandent : « Pourquoi l’attaquez-vous ? Aristote n’est-il pas simplement démodé ?

D’accord, il a dit ces choses horribles sur les esclaves et sur les femmes, mais il n’est qu’un produit de son époque. Le progrès est naturel. Pourquoi vos militants tapent-ils sur des individus comme Aristote ou Newton ? Ils ne sont qu’une étape dans le processus. » Reconnaître qu’il y a des gens mauvais dans le domaine politique ne fait pas débat, mais l’idée qu’il devrait y avoir une certaine moralité dans la science ou la musique est totalement absente.

Aristote ne refléterait-il pas simplement une approche périmée ? Non. Vivant à l’époque de Socrate et de Platon, il est allé délibérément à l’encontre de leurs idées. C’est une lutte de tout temps. Par exemple, ce que nous venons de faire est totalement controversé.

Kepler lui-même l’est tout autant, de même que son œuvre l’Harmonie du monde. Il passe pour démodé, comme Aristote. La plupart des gens disent : « Oui, c’est vrai, dans La Nouvelle Astronomie, Kepler a montré comment les planètes se déplaçaient, c’est génial. Mais ensuite, il est parti dans son délire mystique sur la musique des sphères et autres choses du même genre. Il dit qu’il est connecté à l’univers, ce qui est absurde. » C’est exactement ça. Tu disais, Ben, que la différence entre les planètes observables et celles qui seront découvertes plus tard reflète ce processus de découverte lui-même, ce que Megan avait identifié comme étant la base pour comprendre la manière dont la pensée de Cues progresse en opposition avec celle d’Aristote, et que cette discontinuité est elle-même la substance de l’univers, dans la mesure où elle est la substance même de la progression de notre pensée.

C’est extrêmement controversé ! C’est choquant ! C’est un concept difficile à saisir, mais une fois que vous l’avez saisi, il doit vous mettre un peu mal à l’aise. Une autre chose que je pense importante, vu la nature de la découverte elle-même : le mouvement de l’esprit est visible dans le mouvement des planètes lui-même. Il va de pair avec lui et le dépasse, comme Kepler l’a toujours défendu.

Megan : Je pense que cela ouvre la porte à de nouvelles hypothèses, notamment sur la nature de la dissonance en musique générée par le croisement de plusieurs modes, sur la polyphonie, lorsque plusieurs voix chantent en même temps, ainsi que sur le déplacement de ces différents modes et voix en une seule idée musicale. Cela nous invite à aller encore plus loin, en regardant les dissonances et les ironies, et ces nombreuses autres choses qui sont en résonance avec les principes de l’humanité.