Lyndon LaRouche : petite histoire d’une grande découverte

Avertissement

L’auteur de ces lignes a pris le parti de raconter une histoire.

En l’occurrence, celle du penseur, homme politique et économiste américain Lyndon LaRouche, à l’époque où il travaillait comme consultant industriel.

Plutôt qu’un exposé formel, la démarche vise à familiariser, autant que possible, le lecteur avec la « méthode LaRouche-Riemann », qui fut le fruit de ses travaux.

Pour donner vie à la narration, l’auteur désigne M. LaRouche par son diminutif : « Lyn ».

Par Benjamin Bak, militant S&P, Paris

1956. Lyn rentre chez lui après une nouvelle journée de travail harassante. Cela fait quelques mois qu’il travaille en tant que consultant industriel pour les bureaux new-yorkais de la compagnie George S. May.

La culture et les pratiques de l’entreprise le désarçonnent : elle accorde beaucoup d’importance aux talents de vendeurs de ses cadres supérieurs, ce qui signifie souvent faire prendre au client des vessies pour des lanternes, et fêter la bonne affaire en faisant couler le whisky en abondance.

Cependant, Lyn fait contre mauvaise fortune bon cœur : depuis qu’il est lui-même cadre supérieur, il a accès à une multitude de statistiques provenant du gouvernement fédéral, de la Réserve fédérale (Fed) ainsi que de sources privées on ne peut plus crédibles.

Il dispose ainsi de toutes les informations possibles pour travailler à la conception d’un nouveau type de gestion comptable pour des marchés prospectifs. Cela lui prend un temps considérable, et lorsqu’il s’endort le soir, c’est l’esprit plein du travail accompli.

Il a d’ailleurs l’habitude d’emporter quelques documents pour continuer à travailler chez lui. Il voudrait trouver un moyen de mettre les statistiques disponibles en corrélation avec les réflexions qu’il se fait depuis quelques années sur la fonction de l’énergie dans la croissance économique. [1]

Tout d’abord, il doit interpréter correctement les statistiques, non pas comme des unités auto-évidentes au service d’une analyse comptable coût/bénéfice, mais comme l’expression d’un processus dynamique permettant la reproduction, à des niveaux toujours plus élevés, de la société humaine à travers l’histoire.

1. Le processus de production

Pour cela, Lyn concède que Karl Marx, dont il s’emploie immédiatement à corriger les erreurs axiomatiques, a néanmoins raison sur plusieurs points importants :

1. La source principale de la « plus-value » n’est pas le capital ou la monnaie, mais le travail humain, ce que nous appelons aujourd’hui l’économie réelle ou physique ;
2. Lyn reconnaît que Marx a raison lorsqu’il affirme que « le travail est en premier lieu un phénomène qui se passe entre l’homme et la nature ».

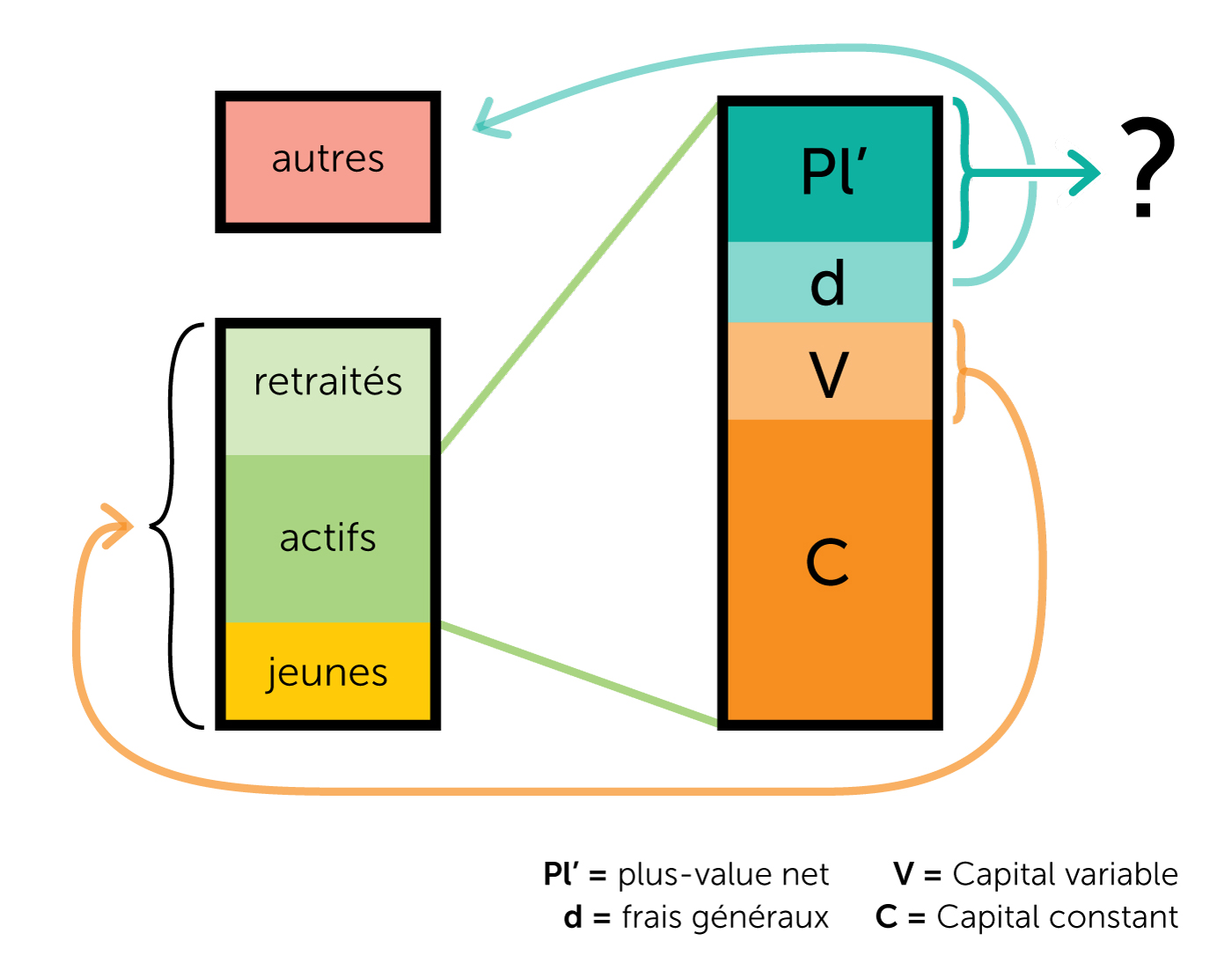
Ensuite, il analyse comment évolue, à différentes périodes, le processus de création de la production totale de la société (Fig. 1), en reprenant à son compte les appellations marxistes de Capital variable (V) et de Capital constant (C) :

• V (Capital variable) : portion de la production allouée à la consommation des ménages et de la population. Dans une économie saine, V doit augmenter.
• C (Capital constant) : portion de la production allouée aux biens d’équipements, c’est-à-dire aux infrastructures de transport, à la production et la distribution d’énergie, aux bâtiments et aux machines.

Enlevons C et V de la production totale (T), il nous reste l’excédent Pl (plus-value), la marge brute d’exploitation dans le système de production. Pl = T- (C+V).

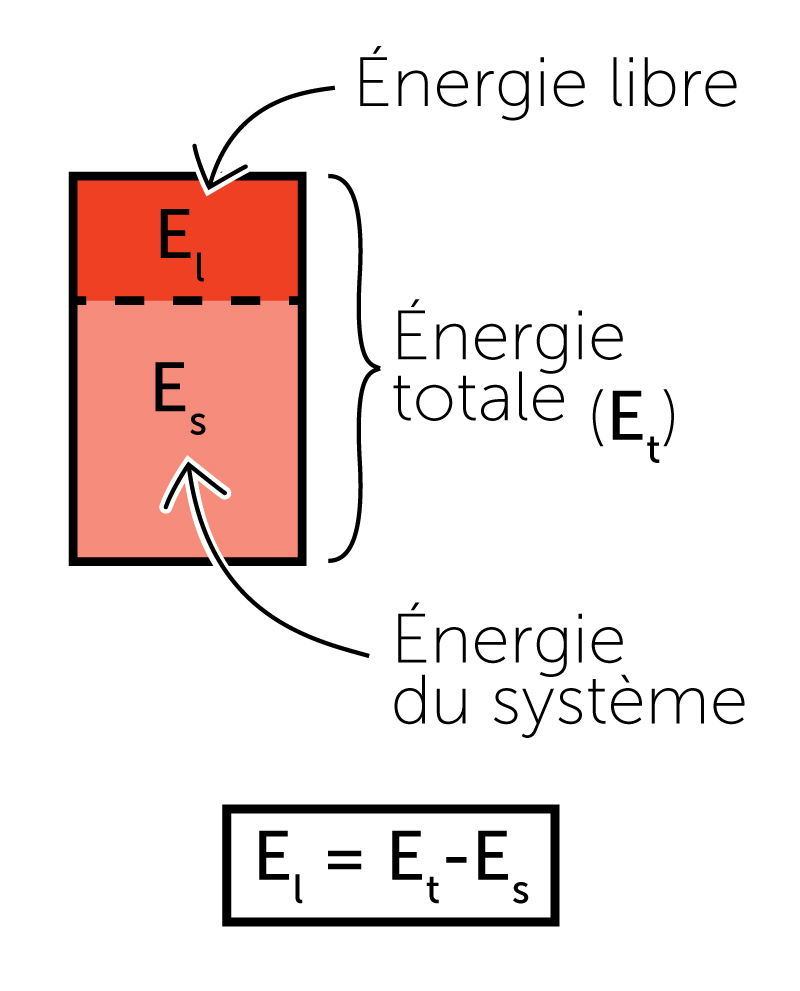
Cependant, pour réellement mesurer « l’énergie libre » du système, il faut réduire de Pl le facteur d, c’est-à-dire les frais généraux du système.

Cela comprend l’administration, le système éducatif, la recherche, la santé, la banque, l’assurance, les professions policières, judiciaires et militaires, ainsi que les professions qui ne sont pas directement liées à la production, mais sont souvent plus qu’utiles, indispensables au bon fonctionnement de celle-ci. [2]

Nous devons de fait retrancher d de Pl, pour créer la nouvelle catégorie, celle de la plus-value nette (Pl’). Ainsi, Pl-d = Pl’.

En organisant notre analyse de cette façon, deux rapports essentiels s’en dégagent :

• Pl’/C+V représente le taux de plus-value ou de « profit », ce taux pouvant également être appelé rapport de l’énergie libre (Pl’) à l’énergie du système (C+V). Dans un système économique en croissance, les trois facteurs de la fonction Pl’/C+V augmentent.
• C/V indique l’intensité capitalistique d’une économie donnée. Dans un système économique sain, c’est-à-dire investissant dans les meilleures technologies plutôt que dans l’exploitation exacerbée de la main-d’œuvre, C augmente plus vite que V.

2. Visualisation

Pour construire la méthode de prévision qu’il recherche, Lyn met Pl’/C+V en ordonnées et C/V en abscisses. Cela amène une question intéressante. Que se passe-t-il quand l’énergie libre (Pl’) est réinvestie dans le système (C+V) ?

Dans un système thermodynamique ordinaire (c’est-à-dire à l’intérieur d’un système fermé), le rapport de l’énergie libre à l’énergie du système baisserait jusqu’à tendre vers 0 (définition de l’entropie).

Or, dans le cas d’une économie basée sur le progrès technologique, ce n’est pas ce qui se passe. [3]

Lyn doit de ce fait rajouter un axe des Z, l’accroissement de la densité de flux énergétique, prenant en compte la progression technologique des machines.

La notion de densité de flux énergétique peut être illustrée à l’aide d’un outil très simple : un couteau. En effet, la pression exercée par l’arête aiguisée de la lame (qui concentre l’ensemble de la puissance sur une toute petite surface) est bien supérieure à la pression exercée par la main sur le manche du couteau.

Cela met à jour un phénomène intéressant : pour exécuter la même quantité de travail, une machine à forte densité de flux énergétique aura besoin de moins de puissance fournie qu’une machine de moindre densité de flux énergétique.

Par exemple, dans le cas de machines à vapeur fonctionnant au charbon, pour accomplir le même travail, telle machine utilisera moins de charbon que telle autre, de conception supérieure et donc plus efficace. [4]

Lyn a besoin d’intégrer dans son modèle l’accroissement de la densité de flux d’énergie, de façon à mettre en évidence l’interaction qui se produit entre les trois paramètres dans le cadre d’une économie moderne. En effet, un simple système de coordonnées cartésiennes ne peut en rendre compte, car dans un tel système, on peut très bien augmenter l’un des paramètres sans augmenter les autres, ce qui n’arrive physiquement jamais.

Pour cela, il va visualiser l’accroissement de la densité de flux énergétique sous la forme d’une action circulaire.

Ce qui donne une fonction spirale conique, l’accroissement de C/V comme rayon du cercle, et de Pl’/C+V comme hauteur (Fig. 2), qui représente l’accroissement du potentiel de densité démographique relatif (Annexe 1).

3. Les ruptures technologiques

Mais ce modèle reste imparfait aux yeux de Lyn : en effet, même dans le cas où il faudrait moins de charbon (par exemple) pour effectuer la même quantité de travail, cela ne ferait que repousser à plus tard l’épuisement des réserves de matière première, et donc l’augmentation du coût social de la technologie utilisée.

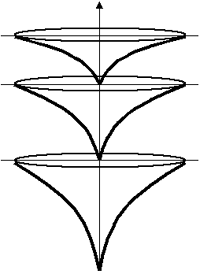
Pour intégrer cette partie du processus, il dut remplacer le cône par un hyper-cône, représentant l’épuisement du processus, l’hyper-cône s’évasant au fur et à mesure de sa croissance et s’étalant horizontalement vers l’infini sans continuer à s’accroître verticalement (Fig. 3).

Cette projection vers l’infini est ce qu’on peut appeler une « discontinuité mathématique ».

Pour surmonter cet épuisement, l’homme ne peut pas recourir au même procédé physique de manière plus efficace, mais se voit obligé d’utiliser un nouveau processus physique plus efficient, une technologie totalement différente engendrée par une nouvelle découverte.

Un second hyper-cône sera ainsi décrit, avec le même processus, puis un troisième, et ainsi de suite. Dans le cas d’une économie « idéale », les intervalles entre les discontinuités diminuent de plus en plus, devançant l’épuisement d’une technologie avant même qu’il ne se produise.

4. Une crise en prévision ?

Lyn aura très vite l’opportunité de tester son modèle de prévision. De 1954 à 1956, l’administration Eisenhower lance une politique d’expansion du crédit à la consommation, pensant permettre une relance industrielle en augmentant de cette manière le pouvoir d’achat des consommateurs.

Dans son rapport, Lyn explique qu’une telle augmentation des frais généraux du système (d) engendrera surtout un accroissement de la production de biens de consommation, mais aucun accroissement de la production de biens d’équipement. De plus, dans le cas du secteur automobile, il constate que deux ans après avoir acheté une voiture à crédit, l’acheteur se retrouve à devoir rembourser encore plus que le prix de la même voiture à l’argus. [5]

Lyn sort de ses pensées en arrivant devant chez lui. Il n’est guère optimiste sur l’avenir proche, ce qui est perçu par ses supérieurs comme reflétant une attitude négative susceptible de perturber la capacité de ses collègues à « faire leur travail ».

Lui-même espère se tromper, tout en sachant qu’il n’a rien laissé au hasard. Il ouvre enfin sa porte et laisse temporairement derrière lui la cécité de ses supérieurs.

Il a des choses beaucoup plus importantes à faire : lancer un mouvement politique à l’échelle internationale pour changer la donne afin que, lors des prochaines crises qui s’annoncent, l’humanité ne finisse pas comme dans les années 1930, avec la bête immonde et une guerre mondiale.

Annexe 1 :
Potentiel de densité démographique relatif (PDDR)

Lyndon LaRouche a été le premier a avoir compris que c’est l’accroissement du potentiel de densité démographique relatif (PDDR) qui définit si une économie est prospère ou en déclin.

Autrement dit, c’est l’augmentation de la « capacité d’accueil » potentielle d’une économie donnée, relative en fonction de la nature de chaque territoire, qui sert de marqueur de la dynamique engagée.

Lorsque feu l’académicien russe Pobisk Kuznetsov eut connaissance de la théorie du potentiel de densité démographique relatif de M. LaRouche, il en fut très heureux et proposa que, tout comme les grandes inventions portent souvent le nom de leur auteur, comme Watt ou Ampère, que LaRouche soit reconnu pour son invention du potentiel de densité démographique relatif, qui sera nommé le « La ».

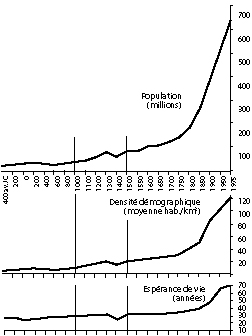
Regardons les trois courbes de la Fig. 4 (évolution de la population européenne depuis 400 av. J.-C.). Il s’agit respectivement :

• des courbes de la population en millions d’habitants,
• de la densité démographique en habitants par km² et
• de l’espérance de vie.

Bien que le préjugé malthusien moderne veuille que la densité démographique s’accroisse au détriment de l’espérance de vie, nous constatons que les trois courbes augmentent simultanément depuis la Renaissance.

Ceci est lié à l’accroissement de la densité de flux énergétique de la société dans son ensemble durant cette période (avènement d’une révolution agricole, urbaine et industrielle), provoquant l’accroissement de son PDDR.

A l’inverse, si le potentiel de densité démographique relatif de la société venait à passer en dessous de la densité démographique réelle, cela aurait un impact négatif sur l’espérance de vie.

Annexe 2 :
Discontinuité mathématique

L’idée de discontinuité mathématique signifie que pour passer du premier hyper-cône au deuxième (Fig. 3), il faut faire une hypothèse qui ne peut être déduite des axiomes existants dans le monde du premier hyper-cône.

Le passage de l’un à l’autre nécessite donc une découverte remettant totalement en cause les axiomes et postulats du système précédent. Poétiquement, on pourrait dire que l’humanité avance, non pas en faisant une série de petits pas, mais par « sauts de grenouille ».

Lyndon LaRouche insiste beaucoup, dans ses écrits, sur la correspondance entre ce type de discontinuité et le principe de métaphore dans la composition artistique classique.

Voir à ce sujet :

• Sur les hypothèses qui servent de fondements à la géométrie, dissertation d’habilitation de Bernhard Riemann ;
• Riemann et les discontinuités mathématiques, Lyndon LaRouche, en EN, Fusion n° 92 sept-oct 2002 ;
• Pourquoi la poésie devra supplanter les mathématiques en physique, Lyndon LaRouche, Fusion Vol. 2, N° 1, p. 11-17, oct 1978. ;
• Découverte d’une fugue de Bach – L’art, notre arme politique, Maëlle Mercier.)

Bibliographie :

• Alors, vous voulez tout savoir sur l’économie ? Lyndon LaRouche, éditions Alcuin, juin 1998 ;
• La France après de Gaulle, Lyndon LaRouche et Jacques Cheminade, 1981 ;
• En défense du sens commun, ou comment s’affranchir de la pensée logico-déductive, Lyndon LaRouche, 1989 ;
• Le Pouvoir de Raison, essai autobiographique, Lyndon LaRouche, éditions Alcuin, 1989 ;
• Riemann et les discontinuités mathématiques, Lyndon LaRouche, Fusion n° 92 sept-oct 2002 ;
• Le rôle de la prévision économique dans la prévision des pandémies, Lyndon LaRouche, 1986 ;
• Pourquoi la poésie devra supplanter les mathématiques en physique, Lyndon LaRouche, Fusion oct. 1978 (Vol. 2, N 1, p. 11-17).