Les trois niveaux de mathématiques

[sommaire]

On dit que le langage étant la base de la pensée, personne ne peut penser sans avoir recours à des mots. Sans examiner ce qu’il peut y avoir de vrai dans cette affirmation, il ne faut pas oublier que la langue change et se développe dans le temps. De nouvelles conceptions naissent quelque part dans les profondeurs de l’esprit humain, et plus tard on leur donne un nom. Que se passe-t-il au niveau des langues mêmes ? Est-il possible que toute une langue puisse naître dans l’esprit d’une seule personne ?

Les toutes premières formes de la langue parlée ne nous sont pas connues. Les observations astronomiques rapportées dans les hymnes védiques, qui furent chantés et transmis de générations en générations bien avant d’être transcrits, permettent de dater ces hymnes à au moins 4000 ans avant J-C. En ce temps-là, le sanscrit était déjà une langue élaborée et complète. La structure fondamentale des langues indo-européennes, y compris l’ensemble des langues modernes européennes, ainsi que le russe et d’autres langues slaves, remonte à des milliers d’années et n’a pas substantiellement changé depuis. Il en va de même pour le chinois et pour des langues sémites comme l’hébreu et l’arabe. En dépit de multiples changements, les langues que parlent les hommes aujourd’hui sont donc très anciennes.

Des origines des mathématiques

Ce n’est pas le cas des mathématiques et de la musique. Les mathématiques — la partie de la langue dont le développement est le plus directement lié à l’accroissement du pouvoir de l’homme sur la nature au cours des 2500 dernières années — ont évolué en une série de révolutions au cours desquelles le contenu et la forme se sont élargis et développés de façon assez imposante. Le développement de la composante mathématique — ou dans un sens plus large géométrique — de la langue, parce qu’il est plus récent, nous est bien plus accessible que les premiers stades de la langue parlée. En étudiant son histoire, nous pourrions espérer découvrir quelque chose de grande valeur sur l’esprit humain.

Survolant les 2500 dernières années de développement des mathématiques, deux événements spécifiques se présentent comme des révolutions de l’espèce la plus radicale.

Le premier se produisit il y a quelque 550 ans, dans le contexte des travaux de Nicolas de Cuse et de l’avènement de la Renaissance en Europe aux XVème et XVIème siècles. Le second, bien plus proche de nous dans le temps, remonte à la notion du transfini élaborée par Georg Cantor il y a une centaine d’années, et culminant dans la découverte par ce même mathématicien de ce qu’on appelle les séries Aleph. Ces deux événements définissent trois niveaux ou domaines au sein des mathématiques, aussi bien du point de vue de son développement historique que de son existence actuelle. Ces trois niveaux de mathématiques correspondent à trois manières différentes de concevoir l’univers.

Le premier niveau, A, est associé, historiquement, avec la géométrie euclidienne des Grecs, celle qu’utilisa par exemple Archimède. Le deuxième niveau, B, est marqué par l’introduction des fonctions dites non-algébriques ou transcendantales et le grand développement engendré par elles. Ce développement commence essentiellement avec Nicolas de Cuse, et sera transmis par les géomètres de la Renaissance tels Brunelleschi et Léonard de Vinci pour éclore pleinement au cours des dernières décennies du XVIIème siècle, notamment dans les travaux de Huygens, Leibniz et Bernoulli. 150 ans plus tard, Riemann enfoncera vigoureusement les limites de ce domaine mathématique et, peu après, Cantor effectuera la percée fondamentale pour entrer dans le domaine du transfini. Le troisième niveau, C, domaine caractérisé par la pensée que reflètent les séries Aleph de Cantor, en est toujours à sa phase initiale.

Je propose de jeter un coup d’œil sur ces trois niveaux, non tant pour en examiner le contenu que pour mieux saisir le changement du mode de pensée qui amène de l’un à l’autre, c’est-à-dire de A à B, puis de B à C.

Avant de rentrer dans le vif du sujet, je souligne que mon objectif n’est pas ici d’être précis de manière formelle. Au contraire, je suis obligé d’employer des expressions plutôt métaphoriques. La nécessité de cette approche deviendra évidente, du moins je l’espère, à la fin.

Deuxièmement, si certaines idées et termes ne sont pas familiers à nombre d’entre vous ici, ne vous laissez pas décourager. Ces sujets sont fondamentalement très simples même s’ils sont profonds ; il est par ailleurs assez difficile de les compacter dans une brève présentation. Si vous ne comprenez pas, n’hésitez pas à interroger des représentants de l’Institut Schiller pour qu’ils vous l’expliquent. N’hésitez pas à les mettre au défi.

Niveau A

La forme de mathématiques dite géométrie euclidienne fut érigée en système déductif logique, aux environs de 300 avant J-C. Bien que les 13 livres des Eléments d’Euclide ne fournissent à bien des égards qu’une représentation déformée et partiale de ce que fut réellement la géométrie grecque, ils suffisent pour mettre en lumière la limite de celle-ci, frontière que Nicolas de Cuse a franchie en lançant la révolution menant vers l’étape supérieure.

La géométrie euclidienne soulève la question de l’organisation de l’espace et de toutes les formes spatiales possibles. Elle tente de réduire ces formes à des éléments fondamentaux dont les relations mutuelles obéissent à certaines règles ou lois. L’élément de base est le point. Cette affirmation est considérée comme une évidence en soi qui ne nécessite pas d’autre interrogation. Le second élément est la ligne droite, ce qui, encore une fois, va de soi. Le troisième élément est le plan. Pour citer une des relations fondamentales entre ces éléments, la géométrie euclidienne postule qu’entre deux points donnés, il existe une ligne droite.

La géométrie euclidienne admet, outre le point, la ligne droite et le plan, un élément additionnel : le cercle, qui est associé à une notion de mesure de longueur ou de distance. La circonférence du cercle serait composée de tous les points éloignés d’une certaine distance précise du point considéré comme le centre. Dans l’espace, la forme correspondante est la sphère. Nous avons donc ces catégories d’objets — points, ligne droite, plan, cercle, sphère.

Maintenant, nous tâchons de construire ou de rendre compte de toutes les formes dans l’espace, à partir de ces éléments. Nous aurons recours immédiatement à la règle et au compas pour ce faire.

Nous commençons par les formes les plus simples : les triangles de divers types. Ensuite nous passons aux rectangles et aux polygones de différents types, puis aux formes solides qui leur correspondent. Nous examinons les relations de proportion et de grandeur, à l’aide de segments définis par paires de points sur une ligne.

Nous trouvons des moyens de diviser tout segment en deux, trois, ou x nombre de segments égaux, d’ajouter et de soustraire des longueurs, de les multiplier et de les diviser selon les lois de la proportionnalité. Toutes ces opérations peuvent être exprimées sous forme sténographique, en termes d’algèbre. Puis, nous passons aux surfaces et aux volumes. Nous découvrons de belles relations comme celle attribuée à Pythagore, à propos des surfaces des carrés formés sur les côtés d’un triangle rectangle, relation qui peut être démontrée en divisant un grand carré de deux façons. (Voir Figure 1).

Cependant, on rencontre très vite, même dans la géométrie euclidienne élémentaire des figures planes, des paradoxes et des anomalies. Ce sont des problèmes qu’on peut formuler facilement, mais qu’on ne peut résoudre en restant dans le cadre de la géométrie euclidienne. Ces anomalies indiquent les limites externes de la géométrie euclidienne.

Par exemple, on rencontre le phénomène de l’incommensurabilité entre des segments de ligne. On peut partager l’étonnement des premiers géomètres qui se rendirent compte qu’il n’existe pas de mesure commune entre la diagonale et le côté d’un carré ; même en les divisant en segments égaux, on ne peut les comparer par des nombres rationnels. Cette prise de conscience a mené à la création d’espèces de nombres différentes, destinées à « remplir » les vides existant entre les fractions et les nombres rationnels.

Une autre anomalie concerne la division d’un cercle en y inscrivant des polygones réguliers. Il est facile de construire un triangle équilatéral dans un cercle, ou un carré, dont les angles divisent la circonférence du cercle en quatre arcs égaux. Nous pouvons aussi construire un polygone régulier à cinq côtés, le pentagone, bien que, curieusement, la construction soit différente d’une façon qui ne peut être complètement comprise que d’un point de vue supérieur. L’hexagone est aussi facile à construire. Mais le suivant, l’heptagone, défie absolument une solution exacte passant par la règle et le compas. Nous nous heurtons là à une limite réelle dans la géométrie euclidienne.

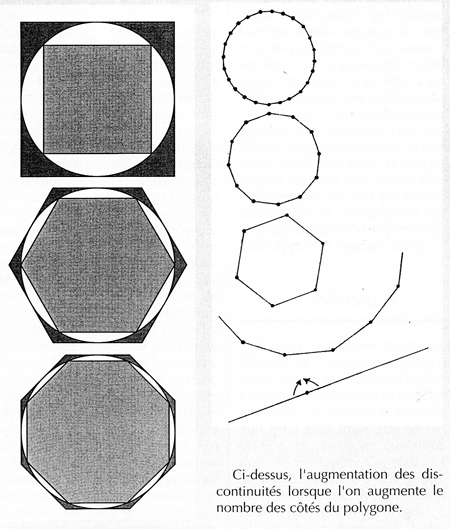
Ce qui nous amène à un autre problème célèbre : la quadrature du cercle (Voir Figure 2). Soit un cercle, comment construire un carré dont la surface est précisément égale à celle du cercle ? Une approche immédiate, qui remonte aux temps anciens, consiste à faire converger un polygone vers la circonférence du cercle en multipliant le nombre des côtés. Pour ceux qui ont une certaine expérience, il n’est pas difficile de diviser un polygone régulier en triangles rectangles, de rassembler ceux-ci en un rectangle, et finalement trouver le côté du carré dont la surface est égale à ce rectangle. Si l’on utilise un polygone inscrit dans un cercle, le carré correspondant sera légèrement plus petit en surface que le cercle ; l’« erreur » correspond à la petite surface comprise entre les côtés du polygone et les arcs de cercles sous-tendus. De même, si l’on circonscrit le cercle par un polygone, on obtient une surface qui est légèrement plus grande. En calculant la moyenne entre les deux surfaces, on obtient une bonne approximation de la surface du cercle. Le géomètre chinois Liu Hui, aux environs de 264 après J-C, en utilisant un polygone de 3072 côtés, avait obtenu une valeur approximative à cinq décimales près.

A notre connaissance, en 250 av J-C, Archimède était le premier à considérer des séries entières· de polygones inscrits ou circonscrits dont le nombre de côtés allait croissant. La procédure la plus simple consiste à commencer par un triangle ou un carré et à doubler, progressivement, le nombre de sommets et de côtés. Il suffit de couper par des bissectrices les arcs ou les côtés correspondants de chaque polygone successif. Ainsi par exemple, en commençant avec un carré inscrit, nous construisons un octogone, un polygone à 16 côtés, à 32 côtés, etc.

Archimède appelait cette démarche la « méthode d’épuisement », et en fait, il est facile de voir que la surface polygonale remplit rapidement la surface circulaire à mesure qu’augmente le nombre de côtés. La surface restante, l’« erreur », est réduite de plus de la moitié à chaque fois que l’on double le nombre des côtés du polygone. En allant aussi loin que possible dans la série de polygones, on peut rendre l’« erreur » aussi petite que l’on veut. Néanmoins — et c’est là qu’est le problème — on n’arrive jamais au point d’avoir éliminé complètement l’« erreur ». Il y aura toujours un léger écart entre le polygone et le cercle.

La situation se complique si l’on prend la sphère à la place du cercle. Dans ce cas, on tentera d’approcher la surface de la sphère à l’aide de polyèdres. Parmi ceux-ci, les plus proches en qualité de la sphère sont les polyèdres réguliers ayant des faces identiques et symétriques. Or, l’on ne peut construire que cinq polyèdres de ce type - les fameux solides platoniciens : le tétraèdre, le cube, l’octaèdre, le dodécaèdre et l’icosaèdre. (Tous peuvent en fait être dérivés du dodécaèdre). Pour les polyèdres, il n’y a aucune procédure de doublement simple, comme on a pu le faire avec les polygones, et certainement aucune qui puisse préserver la propriété de la symétrie. Ici, la différence entre le monde linéaire des plans et des droites, et le monde courbe de la sphère semble prendre une forme très tangible et irréductible.

La révolution de Cuse

Au milieu du XVème siècle, Nicolas de Cuse reprit les travaux qu’Archimède avait faits plus de 1700 ans auparavant, et il poussa sa méthode jusqu’à sa limite conceptuelle. Revenant à la question de l’approche par « épuisement », Cuse demanda si l’on pouvait considérer que les polygones convergent vers l’identité avec la circonférence du cercle. Ou, exprimé sous forme paradoxale, les polygones deviennent-ils égaux au cercle « en arrivant à l’infini » - autrement dit, le cercle est-il un polygone au nombre de côtés infini ? Nicolas de Cuse répond clairement non.

Pour Cuse, la différence entre le cercle et les polygones n’est pas uniquement une question de grandeur, mais de qualité ou de genre. Cuse dit que « puisque les polygones ne sont pas des figures de la même espèce que le cercle, il s’ensuit que, même si l’on peut toujours trouver un polygone qui arrive plus près du cercle que celui qui l’a précédé, parmi les choses qui peuvent être plus petites ou plus grandes, la plus grande absolue ne peut être atteinte en existence ou en possibilité ; la surface du cercle est le maximum absolu par rapport aux surfaces des polygones inscrits, qui peuvent être plus grandes ou plus petites et donc ne peuvent jamais parvenir à la surface du cercle, tout comme aucun nombre ne peut jamais parvenir à la puissance enveloppante de l’unité, ni au pouvoir composite du simple. »

Allons un peu plus loin. A tous les sommets de n’importe quel polygone, les côtés entreprennent un soudain changement de direction, c’est-à-dire qu’il y a une discontinuité, alors que le cercle change constamment de direction, et à cet égard, chaque lieu géométrique du cercle semble être absolument équivalente à l’autre. Ainsi, l’existence de discontinuités à ses sommets distingue le polygone du cercle. Que se passe-t-il quand le nombre de côtés du polygone augmente ? Le nombre et la densité des points de discontinuité provoqués par le changement de direction augmentent. Si, par exemple, on double le nombre de côtés d’un carré 50 fois, on arrive à une situation où un degré d’arc de cercle contient plus de 10 000 milliards de points de discontinuités du polygone. C’est ainsi que si la surface des polygones peut approcher quantitativement celle du cercle, en termes qualitatifs, les deux formes se ressemblent de moins en moins.

Autrement dit, il existe quelque chose d’infime qui différencie le cercle non seulement de chaque polygone individuel, mais de la combinaison ou de la somme de tous les polygones possibles. On ne peut pas lui donner une grandeur spécifiable au sens ordinaire, mais ce quelque chose existe néanmoins. Sa largeur est plus petite que toute quantité ordinaire, mais on ne peut pas parler d’épaisseur zéro. On peut y penser comme la région de transition entre deux mondes, entre deux qualités d’être - où on passe de la « polygonalité » à la « circularité ». C’est ce qu’on appelle une singularité. A partir du monde des polygones, on peut presque atteindre cette singularité, mais on ne peut passer directement dans l’univers du cercle.

Jusque-là, les observations de Cuse semblent être entièrement négatives. Veut-il nous priver de ce qu’Archimède nous a donné ? Mais ajoutons une observation en plus, et nous verrons qu’il nous fournit quelque chose de très précieux. Le fait que le polygone ne peut jamais devenir un cercle, même avec un « nombre infini » hypothétique de côtés, nous oblige à conceptualiser le cercle, et toute la géométrie, de manière différente.

Si le cercle est inaccessible à partir du monde des polygones, d’où vient-il ? En tant que forme, le cercle est la trace d’un mouvement circulaire qui est lui-même le résultat d’une action rotatoire. Cuse considérait l’action rotatoire comme la réflexion la plus directe, dans le domaine visible des formes et des mouvements, de l’être, c’est-à-dire du processus de création de l’univers lui-même. Cette correspondance est démontrée, comme le souligna Cuse, par l’action isopérimétrique ou la moindre action qui est la caractéristique même de l’action rotatoire.

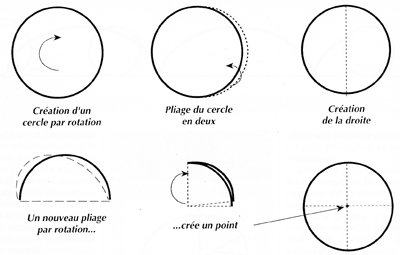
Cette nouvelle vision du cercle place toute la géométrie euclidienne sous un éclairage complètement différent, tout en la dépassant. Nous observons que les formes élémentaires de la géométrie euclidienne sont toutes dérivées de l’action circulaire. (Voir Figure 3). Par exemple, si nous partons de l’action circulaire, nous générons d’abord le cercle. Mais si nous appliquons une fois de plus l’action de rotation au cercle que nous venons de créer, de telle manière que le cercle est plié sur lui-même, alors nous obtenons, en tant que singularité de ce processus de pliage, une ligne droite qui est le diamètre du cercle. Si nous plions encore une fois, nous obtenons un second diamètre qui intersecte le premier pour créer un point. D’autres pliages — qui correspondent à d’autres degrés de rotation — génèrent les sommets des mêmes polygones que nous avons utilisés auparavant pour tenter d’arriver à une approximation du cercle. Un angle n’est également rien d’autre que le résultat d’une rotation. Il apparaît donc que la rotation est partout en géométrie, en tant que substance sous-jacente ; mais en même temps, elle échappe au domaine de la géométrie euclidienne en tant que telle.

Partant de l’observation purement négative de Cuse, qui indique une barrière absolue séparant le cercle de tous les polygones, nous avons brisé les limites de la géométrie euclidienne et commencé à accéder à un domaine supérieur des mathématiques.

C’est là que commence le développement d’un nouveau type de géométrie, où le changement, le mouvement, est élémentaire, et non pas les formes en tant que telles. C’est le mouvement qui fait les formes, et une qualité de changement qui détermine les caractéristiques de ce que nous appelons l’espace-temps.

Niveau B

Si nous examinons les travaux de Léonard de Vinci, que ce soit la construction de machines, l’anatomie, l’hydrodynamique, ou sa conception des ondes de lumière et de son, on voit qu’il était imprégné de la conception géométrique que nous venons de développer. Cependant, l’élaboration formelle d’une géométrie basée sur l’action circulaire commence bien plus tard, avec Huygens, Leibniz et Johann Bernoulli. Leibniz a écrit que cette approche « ouvre la fontaine et le trésor des fonctions non-algébriques ».

A partir de l’action circulaire, et de l’action circulaire uniquement, on forme tout un univers de formes ou d’espèces de mouvement. La construction par Huygens des diverses cycloïdes démontre très bien ce principe.

On prend un cercle et on fait rouler sur lui un second cercle plus petit, soit à l’extérieur soit à l’intérieur. Alors, le mouvement d’un point fixé n’importe où sur le plus petit cercle décrit une courbe dénommée généralement « cycloïde ». (Voir Figure 4). Que se passe-t-il ici ? La courbe est générée par deux degrés d’action circulaire agissant en même temps. D’abord, le centre du petit cercle tourne autour du centre du grand ; et deuxièmement, le petit cercle lui-même tourne. Notez que, lorsque les rayons des deux cercles sont commensurables (leur rapport peut s’exprimer en nombres entiers), les cycloïdes se ferment et les points de singularité — les points de rebroussement — : définissent les positions des sommets de polygones réguliers. Peut-être faudrait-il considérer les polygones comme de simples ombres de ces entités supérieures que sont les cycloïdes fermées. En même temps, il est clair que la majeure partie de la théorie des nombres et l’arithmétique élémentaire se retrouve dans le comportement de ces cycloïdes. Un cas intéressant se présente lorsque les rayons des cycloïdes ne sont pas commensurables. Les points de rebroussement se trouvent alors de manière très dense tout le long du pourtour du plus grand cercle. Dans le cas spécial d’un petit cercle roulant sur une ligne droite considéré comme la circonférence d’un « très grand » cercle, la distance entre deux sommets est égale à la circonférence du petit cercle. A partir de là, ceux qui sont qualifiés en géométrie comprendront facilement comment réaliser la « quadrature du cercle ».

Maintenant que nous avons construit une cycloïde au moyen de cette double rotation, qu’est-ce qui nous empêche de pousser l’expérience plus loin ? Nous pouvons faire rouler un troisième cercle sur une cycloïde, ou bien faire rouler une portion de la cycloïde sur le cercle ou une autre cycloïde. Dans chaque cas, un point fixé sur la courbe en mouvement décrit une nouvelle courbe. Bien sûr, on peut poursuivre ce processus indéfiniment.

Le même principe, sous une autre forme, sous-tend la construction par Huygens de la développante d’une courbe (Voir Figure 5). On prend un cercle, on y attache quelque part un morceau de corde souple et on enroule une portion de cette corde autour du cercle. Maintenant, on déroule lentement la corde tout en la maintenant tendue. Le mouvement du bout de la corde décrit une nouvelle courbe, un genre de spirale, qu’on appelle la développante du cercle original.

A première vue, cette procédure pourrait paraître complètement différente de la génération d’une cycloïde. Mais si nous l’examinons de près, nous trouvons une combinaison de deux degrés d’action rotatoire. En effet, à tout moment du processus, le bout de la corde tourne autour du point auquel la corde touche le cercle. Ce point est momentanément devenu ce que les géomètres appellent le centre de courbure. En même temps, ce centre de courbure se déplace en rotation ! — le long du cercle original. Ainsi, nous avons deux degrés de rotation. Par rapport à la cycloïde, il se trouve en plus que le rayon du deuxième degré de rotation — qui est la distance entre le bout de la corde et le point de contact avec le cercle original s’accroît constamment.

Allant plus loin, nous apprenons à générer des enveloppes de courbes, notamment la fameuse caustique produite par des rayons de lumière réfléchis dans un miroir courbé (Voir Figure 6).

Maintenant, ouvrons un peu plus la « malle au trésor » contenant de nouvelles courbes. Si nous appliquons la procédure de création d’une développante et le roulement d’une courbe sur une autre à la totalité des courbes créées jusqu’à présent, nous produisons une nouvelle génération de courbes ; c’est un processus évolutionniste. Remarquons cependant que l’action rotatoire demeure constamment le « principe héréditaire » sous-tendant le processus de génération.

Maintenant, comme l’a souligné Leibniz, cette famille grandissante de courbes ne peut être décrite par les méthodes de l’algèbre ordinaire. Même dans le cas de la plus simple cycloïde, l’algèbre s’avère inadéquat. C’est pourquoi Leibniz qualifie les nouvelles courbes de « non-algébriques » ou de « transcendantales ». La sténographie algébrique ne sera utilisable que si nous introduisons des symboles et opérations complètement nouveaux comme l’intégrale ou la différentielle de Leibniz. En restant à l’intérieur du monde linéaire de l’algèbre même, il est impossible d’expliquer les nouvelles· courbes ; il faut toujours se baser sur le processus de génération extérieur à l’algèbre ce qui explique en partie pourquoi le calcul de Leibniz provoqua une telle rage chez les mathématiciens, jusqu’à aujourd’hui encore.

Là, nous avons à peine entamé le trésor des fonctions non-algébriques. Maintenant, prenons un cercle, et faisons-le tourner sur n’importe quel diamètre nous engendrons une surface : la sphère ! Fixons un petit cercle perpendiculairement à la surface d’un cercle plus grand, faites tourner le cercle plus grand : nous engendrons un tore. Fixons n’importe quelle autre courbe au grand cercle et tournons ; nous créons l’espèce générale de surface connue sous le nom de surface de révolution. C’est à cette nouvelle source de fonctions transcendantales qu’ont puisé Gaspard Monge et ses collaborateurs de l’Ecole polytechnique à la fin du XVIIIème siècle.

Par exemple, par la rotation d’une droite, nous obtenons des cônes et des hyperboloïdes.

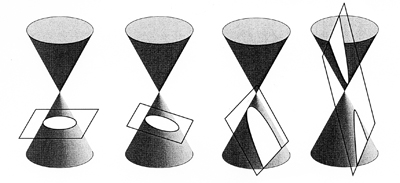
Maintenant, prenons n’importe quelle surface de révolution, et faisons-la intersecter avec une série de plans. L’intersection entre la surface et l’un quelconque de ces plans forme une nouvelle courbe. Les gens calés en géométrie savent qu’en coupant un cône, nous obtenons — selon le choix de coupe — des cercles de différentes tailles, des ellipses, ventrues ou minces, des paraboles et des hyperboles (Voir Figure 7). En coupant le tore ( Figure 8 ), par exemple par des plans parallèles, nous obtenons une famille de courbes d’un ordre plus élevé qui, que je sache, n’a pas encore reçu de nom.

Mais nous pourrions prendre l’une d’entre elles comme base d’un nouveau processus de génération, formant ainsi des surfaces de révolution à partir d’elles, ou produire leurs développantes. Ainsi, une simple courbe peut engendrer, via sa surface de révolution, une famille entière de courbes et d’autres surfaces, et ainsi déjà les contenir dans le sens du potentiel— chose remarquable, si l’on y pense.

C’était une excursion rapide dans le monde des fonctions non-algébriques. Avant de poursuivre notre voyage, permettez-moi de faire remarquer que cette génération de courbes non-algébriques d’un ordre toujours plus élevé permet en même temps d’explorer différentes conceptions possibles de machines.

Dès le moment où nous avons introduit, par l’activité de notre esprit, comme le fit Cuse, la conception d’une nouvelle qualité de changement, et après que l’univers eut indiqué son accord avec cette conception au moyen d’expériences cruciales comme celles réalisées par Léonard de Vinci, et plus tard par Roemer et Huygens dans le cas de la lumière, alors nous sommes prêts pour une révolution technologique. Voilà exactement ce qui est arrivé dans la mise au point rapide de machines, anticipée par Léonard de Vinci et exploitée dans la réalité pendant la révolution industrielle. C’était pour cette raison que Leibniz et Huygens se sont référés aux fonctions non-algébriques en tant que « courbes mécaniques » - ce sont les courbes que décrivent les pièces des machines. Il existe ainsi plus qu’une simple analogie entre la génération d’ordres supérieurs de courbes et de surfaces et le progrès de la technologie.

En réfléchissant à cela, nous devons nous demander quelles sont les limites de ce monde de fonctions non-algébriques. Observons d’abord la chose suivante : l’univers des fonctions non-algébriques est un univers dans lequel le concept de changement est associé à l’idée de mouvement. Mais il existe aussi un concept de changement de qualité du genre de mouvement. Lorsque nous essayons de saisir l’univers physique en termes de concept de mouvement, nous devons définir des genres de qualités de mouvement.

Le développement en espèces est ainsi une caractéristique des fonctions non-algébriques. Nous en avons déjà vu un début dans la distinction que Cuse fit entre les polygones et le cercle. L’élaboration de courbes non-algébriques conduit à une grande multiplicité de nouvelles espèces ou fonctions, et soulève une question fondamentale : est-il possible d’énumérer ces espèces par une sorte de fonction ?

En d’autres termes, supposons pour le moment que le concept d’action circulaire multiplement connexe, de la façon que j’ai indiquée, couvre tous les modes de changement dans l’espace-temps physique. Puis-je maintenant définir cet espace-temps lui-même au moyen d’une fonction qui inclurait toutes les qualités ou espèces de mouvements engendrés par action circulaire ?

Il est également possible qu’il y ait un autre type de changement dans notre univers, qui ne soit pas un mouvement mais pourrait être la cause la plus immédiate du mouvement et du changement dans la qualité du mouvement. Ceci a trait, d’ailleurs, au problème du « champ quantique ».

La tentative d’embrasser l’ensemble des possibilités des fonctions non-algébriques et d’arranger leurs relations en termes d’espèces s’appelle « théorie des fonctions ». Gauss et Riemann, en particulier, réussirent à développer la théorie des fonctions jusqu’à un point qui permit à Georg Cantor d’avoir un aperçu extraordinaire, nous menant dans le monde du transfini.

Il faudra nous contenter de quelques brèves indications pour l’instant. Gauss adopta la méthode consistant à référer toute chose à la sphère, où tout déplacement est de forme rotatoire. Ceci conduit entre autres choses à ce qu’on appelle le domaine complexe. Lorsque nous redéfinissons les fonctions transcendantales en termes de ce domaine sphérique ou complexe, nous éliminons certains aspects artificiels de l’espace euclidien ordinaire, et l’organisation interne de ces fonctions se révèle merveilleusement. Prenant la suite de l’œuvre de Gauss, Riemann montra comment caractériser une fonction dans le domaine complexe, entièrement par le type et la configuration de ses singularités, sans référence aux grandeurs scalaires. Ceci réduit la détermination des espèces de fonctions transcendantales à un problème d’analysis situs (topologie).

Riemann essaya aussi de caractériser le processus par lequel une fonction peut « sauter » d’une espèce inférieure à une espèce supérieure. L’introduction d’une nouvelle singularité dans une fonction correspond au cas où un processus physique conduit à, et au-delà, de ses limites comme apparemment déterminées par des taux finis de propagation d’action dans ce processus. A ce point, nous avons ce que les physiciens appellent un changement de phase. Certaines qualités nouvelles surgissent dans ce processus, accompagnées — dans les bons cas, néguentropiques — par un accroissement du nombre de degrés de liberté. Riemann montre comment une fonction peut être construite, qui passe par toute une série de changements de phase, de l’espèce ou l’état S1 à l’état S2, puis S3 et ainsi de suite.

A peu près à la même époque, Riemann, Weierstrass et quelques autres poussaient le concept général de « fonction » à ses limites. Quelle serait une sorte très générale de fonction mathématique complètement arbitraire ? Est-il possible de comprendre l’espèce la plus générale de courbe par quelque méthode uniforme de représentation ? La principale forme de représentation que les gens prirent en considération fut la série dite de Fourier. Essentiellement, la méthode de Fourier consistait à expliquer les changements à l’intérieur d’une fonction donnée en termes de changement des phases relatives d’un très grand nombre de processus cycliques - un genre de cycloïde multiple généralisé.

La révolution de Cantor

Cantor commença son œuvre sur la théorie des fonctions en étudiant le problème consistant à représenter une fonction arbitraire par la série dite de Fourier et il découvrit que cette représentation de Fourier ne convient en général pas : il y aura généralement un domaine singulier sur lequel une fonction donnée est en désaccord avec sa série de Fourier. Alors, comme l’indiqua Cantor, nous pouvons ordonner les espèces de fonctions selon leur degré de non-représentativité, exprimé par la densité de singularités dans chaque intervalle. Ceci implique que les espèces de fonctions ont une façon naturelle de se ranger ou de s’ordonner selon des densités croissantes de singularités.

Nous avons déjà vu ce genre de choses dans notre discussion sur le cercle et les polygones. Chacun de ces polygones représente une espèce, ayant 4, 8, 16, et ainsi de suite, singularités. Ces espèces sont naturellement ordonnées par ordre croissant de la densité de leurs singularités, les sommets, sur la circonférence du cercle.

Observons aussi que chaque espèce contient la précédente dans le sens suivant : nous pouvons immédiatement obtenir le carré en reliant un sommet sur deux d’un octogone, par exemple. Notez également que chaque espèce supérieure est obtenue, par une simple action de doublement du nombre de côtés.

Maintenant, nous avons observé que le cercle se trouve, pour ainsi dire, au-dessus de toute série d’espèces de polygones et peut les générer en termes d’action circulaire. Ainsi, l’ordonnancement serait apparemment terminé si nous ajoutions, pour ainsi dire après toutes les espèces polygonales ; les espèces circulaires :

[P4, P16, P32, ... ], ? , C

Les crochets contiennent tout le système ordonné d’espèces de polygones dont le nombre de côtés est une puissance de deux. Cuse insiste que le cercle est absolument séparé de chacun et de la somme des polygones. Ceci suggère la question de savoir s’il ne pourrait pas y avoir d’autres espèces situées dans l’« espace » entre le cercle et les polygones. Cantor répond clairement « oui » à cette question. Sans essayer de former une image concrète de ce à quoi cela pourrait ressembler, imaginons simplement une espèce hypothétique S qui est « la première espèce après ou au-dessus de tous les polygones » et représente seulement cette portion de la puissance d’action universelle qui suffit exactement pour générer tous les polygones.

On pourrait capter quelque chose de cette situation dans un dessin en perspective d’un train disparaissant au loin comme pour essayer d’atteindre une étoile, mais convergeant à la place à un point de fuite à l’horizon, au-dessous de l’étoile, qui est encore infiniment loin. Le point de fuite est l’espèce S, l’étoile est l’action circulaire.

Ce que Cantor fit alors, c’est développer ce que nous pourrions appeler une théorie générale de types d’ordonnancement d’espèces. Dans cette théorie générale, nous laissons complètement de côté la nature particulière des espèces en cours d’ordonnancement, et examinons seulement la manière dont elles sont ordonnées l’une par rapport à l’autre. Nous appliquons ainsi la méthode de Leibniz appelée « analysis situs ».

Commençons par une simple série d’espèces S1, S2, ..., Sn dans laquelle S2 est le successeur naturel de S1, S3 le successeur naturel de S2, etc. De telles séries peuvent continuer indéfiniment, comme les polygones, ajoutant des degrés de liberté à chaque étape.

Maintenant, la qualité de changement incorporé dans la série S1, S2, S3, ..., qui est la cause immédiate de la progression de chaque espèce jusqu’à la suivante, constitue une espèce supérieure à chacun des termes individuels de la série. Appelons cette espèce supérieure S’. A la suite de Cantor, nous plaçons S’immédiatement au-dessus ou après la série S1, S2, S3, ... comme son successeur naturel : [S1, S2, ...], S’

Observons quelque chose d’intéressant, que Cuse a déjà signalé à propos du cercle et des polygones : il semblerait qu’un nombre littéralement infini d’étapes sépare la première espèce S1 de l’espèce supérieure S’. Ce genre d’infinité numérique n’est vraiment qu’un reflet paradoxal du fait que S’ ne puisse pas être atteintà partir de l’une quelconque des espèces Sn prises en elles-mêmes c’est-à-dire séparées du principe créateur universel (l’absolu) qui est le même en toutes choses et se situe au-dessus de tout.

Maintenant, l’espèce S’, n’étant pas l’absolu, est elle-même capable de développement. Maintenant, nous pouvons commencer à comprendre pourquoi Cantor utilisa le terme « transfini » pour décrire ce genre d’ordonnancement. Ainsi, en commençant par S’, nous avons une série S’1, S’2, S’3, ... qui suit immédiatement la série précédente dans l’ordre.

[S1, S2, ...], S’1, S’2, S’3, ... Une fois encore, il y aura une prochaine espèce supérieure S’’, qui incorporera le principe de changement engendrant cette deuxième série et constituera la prochaine espèce après cette série : [S1, S2, ...], [S’1, S’2, ...], S’’.

Nous pourrions continuer comme ça jusqu’à S’’’ , S’’’’ etc., mais le principe est clair. Réfléchissons à cela un moment : « le principe est clair ». Déjà, notre esprit a formé le concept d’une série supérieure S, S’, S’’, S’’’ ... qui transcende la première série originale, et la seconde, troisième et quatrième dans notre ordonnancement, et ainsi de suite. Cette série supérieure incorpore elle-même une qualité supérieure de changement, une espèce que nous pourrions appeler T, qui est hors d’atteinte de chacune et de toutes les espèces-S, et forme leur successeur nécessaire dans l’ordonnancement.

[S1, S2, ...], [S’1, S’2, ...], [S’’1, S’’2, ...], [S’’’1, S’’’2, ...],T

Schéma de la série croissante

Mais T, bien sûr, commence une nouvelle série, etc. Nous explorons le tout début de ce que Cantor appelait la seconde classe de nombres.

Une nouvelle idée se forme bientôt dans notre esprit. Tout le processus par lequel nous avons commencé à partir de la première espèce S1 et sommes finalement arrivés à T, pourrait s’appliquer à T aussi ! Bien sûr, cela ne serait pas littéralement le même processus, mais ce serait équivalent dans le sens du concept de Leibniz de l’analysis situs. Ainsi, d’un point de vue formel, nous pouvons adjoindre à « T » un autre exemplaire de tout l’ordonnancement, où nous remplaçons simplement S par T partout. La prochaine espèce supérieure, incorporant la qualité de changement de toute la série T, nous pourrions l’appeler U.

Ah ! Si nous pensons à tout le processus allant de S à T comme un type spécifique de transformation, et que le même type nous conduit de T à un niveau U encore supérieur, alors nous avons le concept d’une série S, T, U, V etc. et avons une qualité de changement incorporée dans toute cette série, qui est au-dessus de tous les processus dont nous avons discuté jusqu’à maintenant. Nous voyons déjà le chemin qui mène au prochain niveau supérieur de développement transfini.

Pour poursuivre cette exploration, et éviter d’avoir le vertige et de tomber dans le ravin, nous aurions besoin d’une « carte » du genre global d’ordonnancement qui surgit. C’est ce que Cantor a fourni (ou du moins a-t-il essayé) avec sa théorie des types ordinaux transfinis et un mode spécial de notation, qui joue vis-à-vis des ordonnancements transfinis un rôle semblable au système décimal pour les nombres ordinaires. Quoi qu’il en soit, ce développement formel n’est pas essentiel pour nous ici.

Vous reconnaissez peut-être une similarité entre ce que nous faisons et ce que Leibniz, Huygens et Gaspard Monge firent en ouvrant la fontaine des fonctions non algébriques. Il se produit un processus semblable lorsque nous explorons le Motivfuehrung et le principe des variations en musique. En fait, le transfini de Cantor n’est rien d’autre que l’analysis situs, les principes d’ordonnancement sous-jacents de toutes ces sortes de processus de développement. Mais je n’en suis pas encore arrivé au point essentiel. Tout cela n’est qu’un échafaudage. Nous avons commencé par nous demander s’il était possible d’énumérer toutes les espèces possibles au moyen d’une simple fonction mathématique ; Riemann et quelques autres posèrent implicitement ce problème. La réponse à cela, prodigieuse, ouvre la voie aux fameuses séries d’alephs de Cantor, dernière étape de notre voyage.

La révolution des alephs

Réfléchissons à nouveau brièvement au genre de processus que nous avons commencé à déclencher. A tout point de ce processus, il serait possible d’énumérer, implicitement, l’ordonnancement des espèces englobé jusqu’à ce point ; il suffit de retracer les étapes précédentes. Mais qu’en est-il du principe qui continue à nous amener à poursuivre le processus plus loin ? Nous faisons avancer le processus en formant, dans notre esprit, le concept d’une nouvelle qualité de progression, que nous nommons par une fonction mathématique. En élaborant le processus, nous devenons conscients de ses limites ou de sa relative finitude, et en même temps un nouveau concept se forme. Mais dès que nous avons conceptualisé une direction de développement en termes d’une fonction - c’est-à-dire une progression ordonnée telle que nous l’avons indiquée - c’est précisément à ce point que commence une nouvelle phase de développement par delà cette fonction.

Ah ! Cela signifie que le potentiel, le pouvoir de ce processus de formation de concepts transcende le concept de fonction lui-même — au moins dans le sens donné au mot fonction au niveau « B » de mathématiques. A la suite de Cantor, nous appelons « Aleph zéro » la puissance de cette notion ordinaire de fonction, énumération ou succession ordonnée de valeurs. Ensuite, nous appelons « Aleph Un » la puissance du concept d’un principe de génération du processus transfini que nous venons juste de décrire, par un processus de conceptualisation de fonctions d’ordonnancement toujours supérieures, un processus qui par sa nature même transcende toute autre fonction.

Maintenant, observons que l’Aleph Un est le successeur nécessaire de l’Aleph Zéro, bien qu’ils soient séparés par ce qui semblerait être un fossé incroyablement profond et infranchissable.

Observons aussi que l’Aleph Un est absolument inatteignable par quelque forme de langage que ce soit. Nous ne pouvons pas le communiquer directement, linéairement, mais nous pouvons toujours provoquer son apparition dans les processus mentaux créatifs de l’esprit d’une autre personne. L’Aleph Un n’est, dans ce sens, communicable que par métaphore.

Pourtant — et cela est crucial — l’Aleph Un est un objet-pensée très précisément défini. Ce n’est pas une action créatrice ou un processus général de formation de concepts créateurs, dans un sens très vague ; ce n’est certainement pas Dieu. Mais c’est un objet-pensée immédiatement au-dessus de toute notion ordinaire de fonction mathématique, et qui engendre immédiatement cette notion. Nous pourrions dire que l’Aleph Un est un exemple de niveau de réalité physique qui limite immédiatement l’espace-temps ordinaire de l’extérieur.

En faisant maintenant de cette couche limite un objet de conscience, nous amenons la physique dans un nouveau domaine, vers une renaissance scientifique.

Dans un sens, le concept de fonction hérité du niveau « B » de mathématiques joue maintenant le rôle que les polygones jouèrent pour Nicolas de Cuse. Ceci nous dit également que l’espace-temps habituel de la physique mathématique d’aujourd’hui est extérieurement limité par quelque chose d’autre, que nous commençons maintenant à conceptualiser.

Nous en sommes arrivés au stretto.

Dois-je vous dire qu’il y a des Alephs supérieurs et en fait toute une série transfinie d’Alephs ?

Pensons au saut d’« Aleph Zéro » à « Aleph Un ».

Je pense que cela caractérise très bien la percée révolutionnaire de Cantor du niveau « B » de mathématiques, le domaine de la théorie des fonctions, au nouveau niveau « C », la fontaine et le trésor du transfini.

Maintenant, comparons cette percée à celle que fit Nicolas de Cuse, du niveau « A » au niveau « B ». N’y a-t-il pas un genre d’équivalence supérieure entre ces deux révolutions ? Maintenant, revenons à ce que Lyndon LaRouche a écrit sur l’hypothèse supérieure et faire l’hypothèse de l’hypothèse supérieure.

Est-ce que cela ne suggère pas que nous sommes au seuil d’une nouvelle renaissance ? Les premiers pas ont déjà été parcourus.

On objecterait peut-être : Quoi ? Une nouvelle renaissance ? Vous êtes fou ? Mais je ne l’ai pas vue à la télévision ! Nous ne la verrons pas, au moins pas au début. Mais n’oublions pas : les graines précèdent les fleurs. Et nous les plantons maintenant.