Sébastien Drochon : Gödel et l’heureuse incomplétude

Intervention de Sébastien Drochon, responsable de Solidarité & Progrès, lors de la conférence organisée par S&P et l’Institut Schiller à Paris, les 8 et 9 novembre 2025.

Introduction

Ce que je veux présenter ici ce matin est un travail exploratoire visant à ouvrir des pistes de réflexion sur le travail de Lyndon LaRouche (1922-2019) en économie physique, à partir d’une lecture d’un de ses textes, datant de 1993, et qui s’intitule justement La Découverte de LaRouche.

Je ne vais pas aborder tous les aspects de ce texte extrêmement dense. D’ailleurs, mes compatriotes, après moi, en développeront certains.

J’aimerais porter mon attention sur une des idées développées par LaRouche : la différence fondamentale entre un processus de pensée purement logique et déductif, et celui qui caractérise la véritable créativité, à savoir, celui de briser la logique pour la transcender.

Pour cela, je voudrais m’appuyer sur le théorème d’incomplétude de Kurt Gödel, ce mathématicien de génie qui vécut au XXe siècle.

Pourquoi ce théorème de Gödel est-il si fondamental ?

Eh bien, parce qu’il montre en quelque sorte que la créativité humaine ne peut pas se réduire à des raisonnements algorithmiques. Et ce qui est drôle, c’est qu’il le démontre justement par des mécanismes de raisonnement algorithmiques.

Ce qui fait que ceux qui prétendaient pouvoir un jour TOUT prouver par des raisonnements algorithmiques ou arithmétiques, ont dû se rendre à l’évidence que l’arithmétique elle-même prouvait le contraire. Dur dur !

Le roi lui-même se pointe du doigt face au miroir et déclare : « Je suis nu ! »

Mais je sens déjà qu’en parlant de mathématiques, je vais perdre quelques-uns d’entre vous et je comprendrais totalement.

Je vous rassure donc, nous n’allons pas ici faire de grandes démonstrations arithmétiques, quelques additions et multiplications tout au plus, et certainement pas d’intégrales triples, sinon, au milieu même de ma présentation, je serai certainement le premier à sortir de cette salle.

La cohérence d’un système d’axiomes

Après cette NON-brève introduction, entrons dans le vif du sujet.

Je me concentrerai ici sur ce que l’on nomme le Premier théorème d’incomplétude de Gödel, qui se résume de la manière suivante :

Ok…On va expliquer un peu tout cela.

Qu’est-ce qu’une démonstration ? C’est une suite d’affirmations qui se déduisent par pure logique à partir de ce que l’on appelle des axiomes. Et les axiomes, ce sont des briques de base, des vérités admises a priori, à partir desquelles on construit nos démonstrations et théorèmes.

Prenez cet exemple d’axiomes simples :

A partir de cet ensemble d’axiome, je peux construire une démonstration comme :

Et

Si je pars du principe que les axiomes de base sont vrais et que j’en déduit un énoncé, cet énoncé est « forcément » vrai.

Le rêve serait donc de trouver un système d’axiomes cohérent, si parfait qu’il permettrait de démontrer TOUTES les vérités mathématiques.

Le Graal en quelque sorte.

Or, il arrive souvent que des systèmes d’axiomes aboutissent à des contradictions ou à des absurdités.

Si cela vous intéresse, je pourrai, pendant la pause déjeuner, vous démontrer que 1 = 2, mais je ne vais pas le faire maintenant.

Je prendrai comme exemple le système d’axiome précédent et y ajouterai deux autres axiomes :

On peut désormais en déduire que Socrate est aussi immortel alors qu’on en avait déduit auparavant qu’il était mortel ! Il y a là une contradiction.

Le problème vient, semble-t-il, de l’axiome 5, car de quelle mortalité ou immortalité parlons-nous ici ? Et comment résoudre ce paradoxe ?

Dans notre langage, la poésie nous permet de résoudre ce paradoxe. L’ambiguïté pousse l’esprit à dépasser les faiblesses axiomatiques, à penser au-delà. A identifier directement un principe supérieur qui distingue une certaine idée d’immortalité d’une autre, par exemple. Ou du moins à chercher dans cette direction.

Mais en mathématique, où les définitions des termes ne doivent souffrir aucune ambiguïté, on cherchera à ajouter d’autres axiomes pour annihiler cette incohérence. Et ceci, en prenant le risque de provoquer de nouvelles incohérences par la suite. Un peu comme quand vous essayez de construire un château de cartes….

Évidemment, l’incohérence, le paradoxe, c’est l’enfer du mathématicien. Il cherchera toujours à s’assurer qu’un système reste intrinsèquement cohérent. Sans quoi il ne peut rien prouver et ne peut donc, de son point de vue, arriver à TOUT prouver.

Une petite parenthèse

En mathématique, des systèmes d’axiomes différents peuvent coexister.

Prenez la géométrie euclidienne avec ses axiomes et postulats de base. Avec eux, on démontre par exemple le fameux théorème de Pythagore, ou encore celui qui stipule que la somme des angles d’un triangle est toujours égale à 180°.

Cependant, au fur et à mesure que les mathématiques ont avancé, il a été nécessaire de construire d’autres géométries NON euclidiennes, en modifiant un des postulats. Le fameux postulat des parallèles.

En effet, si l’on définit une ligne droite comme le chemin le plus court pour aller d’un point à un autre, le parcours ne sera pas le même si l’on se trouve sur un plan, une sphère ou une surface en forme de selle de cheval.

Dans chacun de ces trois cas, la somme des angles du triangle est soit inférieure, soit égale ou supérieure à 180°.

D’un point de vue purement formel et mathématique, savoir quel système d’axiome est le plus valable ne se pose pas. En mathématiques, on prend celui qui nous arrange selon ce qu’on désire démontrer. Selon la « géométrie » dans laquelle on se trouve. Par contre, quel système choisir pour décrire l’univers physique réel, ça c’est une autre histoire… Qui sera peut-être abordée plus tard…

Je ferme la parenthèse.

Revenons à nos moutons arithmétiques

Le but de mon propos est de montrer que cette question des systèmes d’axiomes, de leur cohérence et de leur capacité à démontrer des problèmes qu’on n’a, jusqu’ici, pas réussi à démontrer, a toujours été en quelque sorte centrale pour des mathématiciens désireux de trouver la pierre philosophale, le Graal nous indiquant le chemin de toute La connaissance, du moins en mathématique.

Et à la fin du XIXe siècle et au début du XXe, de grands mathématiciens continuaient à sérieusement se pencher sur cette problématique. Certains, comme David Hilbert, embrassait le rêve qu’on concevrait un jour, en arithmétique du moins, un système parfait d’axiomes simples et vrais permettant :

• de démontrer TOUT ce qui est vrai, donc permettant de faire que TOUTE proposition vraie soit démontrable ;
• de réfuter TOUT ce qui est faux, donc permettant de faire que TOUTE proposition fausse soit réfutable.

Hilbert faisait partie des mathématiciens persuadés que tout problème posé pouvait être résolu avec du temps, de la patience et des efforts suffisants. Il avait présenté, lors de la conférence inaugurale du IIe congrès international des Mathématiques à Paris en 1900, une désormais célèbre liste de 23 problèmes qu’il prédisait être le moteur d’une grande partie de la recherche mathématique tout au long du XXe siècle.

Il y avait là tout un débat philosophique entre différentes approches sur lequel je ne m’étendrai pas. Toujours est-il qu’au début des années 30, Hilbert était persuadé que son approche était la bonne et qu’on arriverait définitivement à asseoir les mathématiques sur un socle inamovible et permanent permettant de TOUT démontrer.

Alors même que la partie semblait gagnée pour Hilbert, un jeune doctorant du nom de Kurt Gödel allait faire s’effondrer le projet de toute une vie en affirmant ce que je vous ai mentionné plus avant et que je reformule ici :

L’angoisse…

Pire que le vide, l’indécidable... Mais voyons ce qu’on entend par des propositions arithmétiques INDÉCIDABLES.

Un exemple simple est ce qu’on appelle la Conjecture de Goldbach (du nom du mathématicien allemand Christian Goldbach, qui vécut entre le XVIIe et XVIIIe siècle), qui stipule :

Les nombres premiers étant ceux qui ne peuvent être divisés que par 1 ou eux-mêmes tels que 2, 3, 5, 7, 11, 13, 17, etc.

En effet, si l’on regarde les premiers nombres pairs après 4, on a :

Cette propriété se vérifie jusqu’à des nombres gigantesques de l’ordre de 10 puissance 18, à savoir des nombres à plus de 18 chiffres, mais on n’a toujours pas trouvé de preuve pour l’ensemble infini des nombres pairs.

Mais bon ! si c’est vérifié jusqu’à de tels nombres, c’est que c’est “certainement” vrai !

Certes, mais c’est sans compter avec l’exception qui INFIRME la règle.

Prenons une autre conjecture de Goldbach qui dit la chose suivante :

Voyons ce que cela donne pour les premiers nombres impairs supérieurs à 3 :

Et cela se vérifie au-delà de 1000, 2000, 3000, 4000, 5000… seulement voilà :

On sait donc désormais que la deuxième conjecture est FAUSSE.

Alors que pour la première, on ne peut aujourd’hui affirmer ni qu’elle est vraie, ni qu’elle est fausse. Elle est dite INDÉCIDABLE.

Et il en va de même pour de nombreux problèmes en mathématique, qui n’attendent qu’à être démontrés ou réfutés, et qui restent pour l’instant dans la catégorie des indécidables.

Hilbert voulait se convaincre que toute proposition encore indécidable finirait par être découverte et qu’à la fin, on réussirait à faire en sorte qu’il n’y ait plus aucune proposition indécidable.

Mais Gödel fait alors tomber l’édifice de cette théorie en démontrant, par l’arithmétique elle-même, qu’il existera toujours des propositions INDÉCIDABLES, quel que soit le système d’axiome que l’on aura construit.

En résumé, UNE arithmétique ABSOLUE n’existe pas. Elle sera forcément INCOMPLÈTE. D’où le terme « théorème d’incomplétude ». Et le pire, c’est que c’est l’arithmétique elle-même qui le prouve !

Le roi se montre du doigt et déclare : « Je suis nu ! »

Penser au-delà, l’univers physique

Mais rassurez-vous, avec son théorème, Gödel ne prétend pas prouver que rien n’est connaissable. Au contraire, comme l’a dit dernièrement le pape Léon XIV en prenant l’exemple de Nicolas de Cues et son principe de « coïncidence des opposés » :

Ou, pourrions-nous dire, « parce que nous ne connaissons pas toutes les réponses ».

La découverte de Gödel montre que la connaissance ne passe pas par une multiplicité de savoirs absolus et figés qu’on cherche à combiner mécaniquement pour construire une soi-disant représentation du monde, une théorie absolue du tout.

Au contraire, à l’instar des polygones inscrits dans le cercle, et que l’on cherche à rapprocher du cercle en multipliant les côtés, alors même que le cercle est d’une nature distincte, régie par un principe d’unité supérieure, la logique déductive, en tentant de compléter les systèmes d’axiomes, ne permet pas d’appréhender l’unité supérieure des principes physiques qui gouvernent l’ensemble de notre univers.

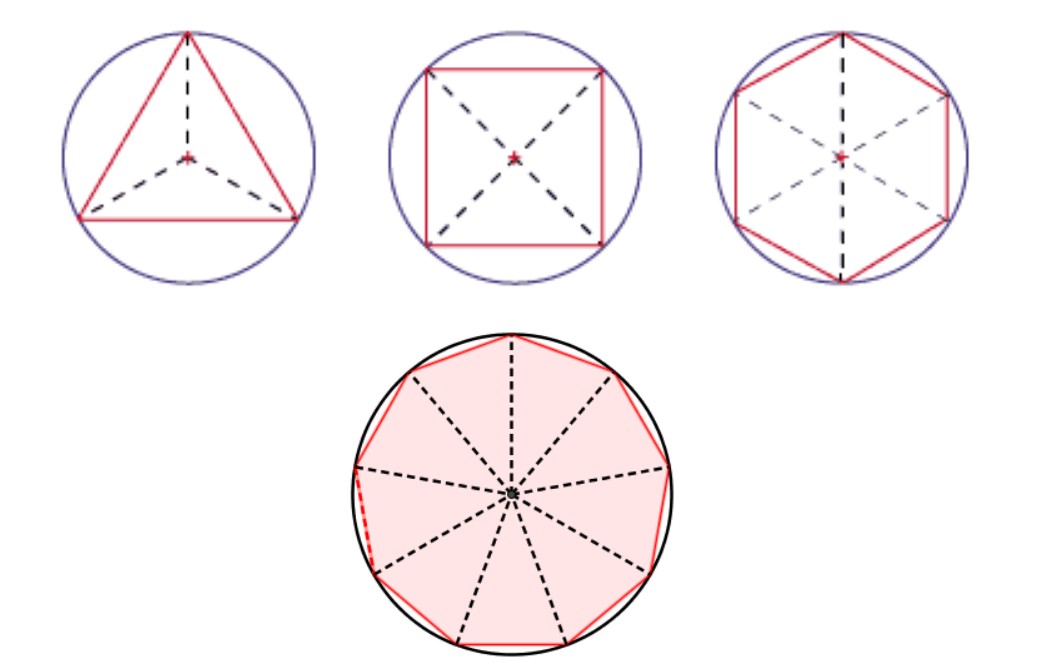
Comme pour passer du monde des polygones au cercle, il nous faut effectuer des sauts conceptuels qualitatifs dans notre manière de penser, générer une discontinuité dans la pensée que la pure logique ne peut appréhender.

Réduire l’esprit humain à un simple algorithme devient donc non seulement réducteur mais même destructeur.

Car nier sa capacité à transcender les limites de ses premières théories pour élaborer de nouvelles idées, émettre des hypothèses et les vérifier par l’expérience, c’est nier la capacité de tout être humain à exercer volontairement son pouvoir de raison pour faire des découvertes scientifiques fondamentales et améliorer ainsi la capacité de vivre et de croître de son espèce.

De ce point de vue, je trouve que la découverte de Gödel a de profondes implications pour permettre d’appréhender cette approche de l’économie physique telle que l’a précisément définie Lyndon LaRouche.

Explorer le monde physique, au-delà de la pure mathématique logico-déductive, voilà ce qui est plus que tout nécessaire pour assurer le progrès de l’humanité.

Gödel, qui s’était lié d’une grande amitié avec Albert Einstein lorsqu’ils étaient tous deux à Princeton, et qui a d’ailleurs écrit au sujet de la Relativité, n’aurait certainement pas dit le contraire.

Sur ce, je laisse la parole à mes compatriotes pour élaborer la suite.

Merci.